こんにちは
こいパパです( ̄▽ ̄)
今回は三角形の面積、多角形の面積を学び直していきます(*^_^*)
三角形の面積
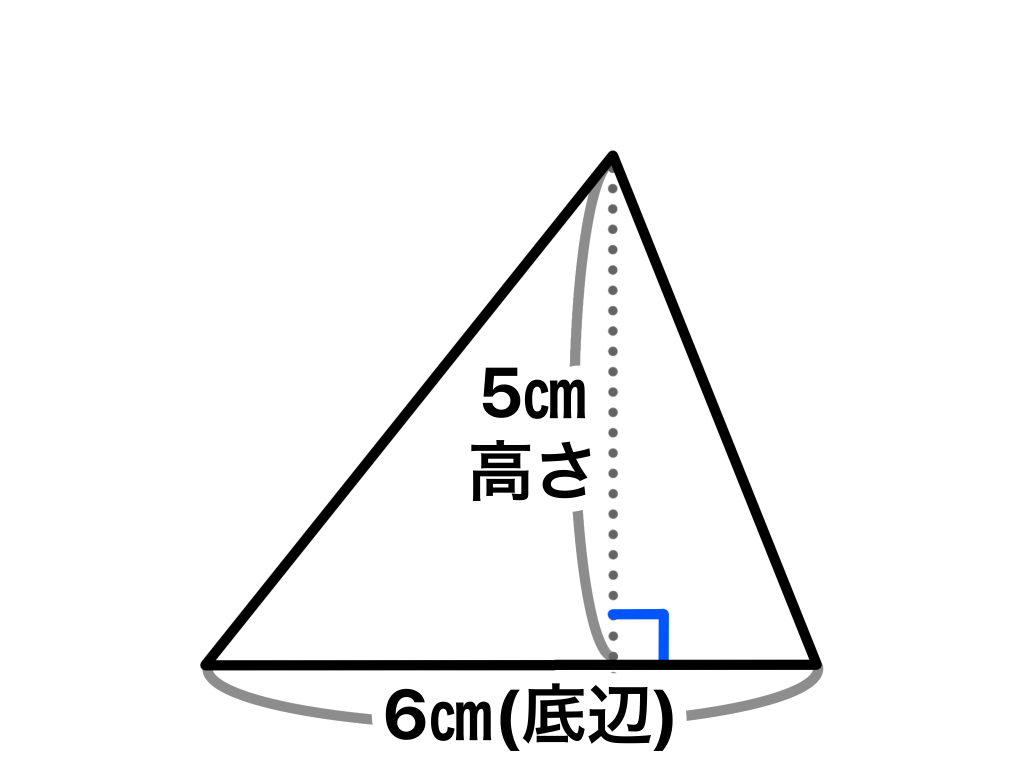
三角形の面積は
底辺×高さ÷2
で求めることができます( ̄▽ ̄)
では何故この求め方で三角形の面積が求められるのか考えてみましょう(*^▽^*)
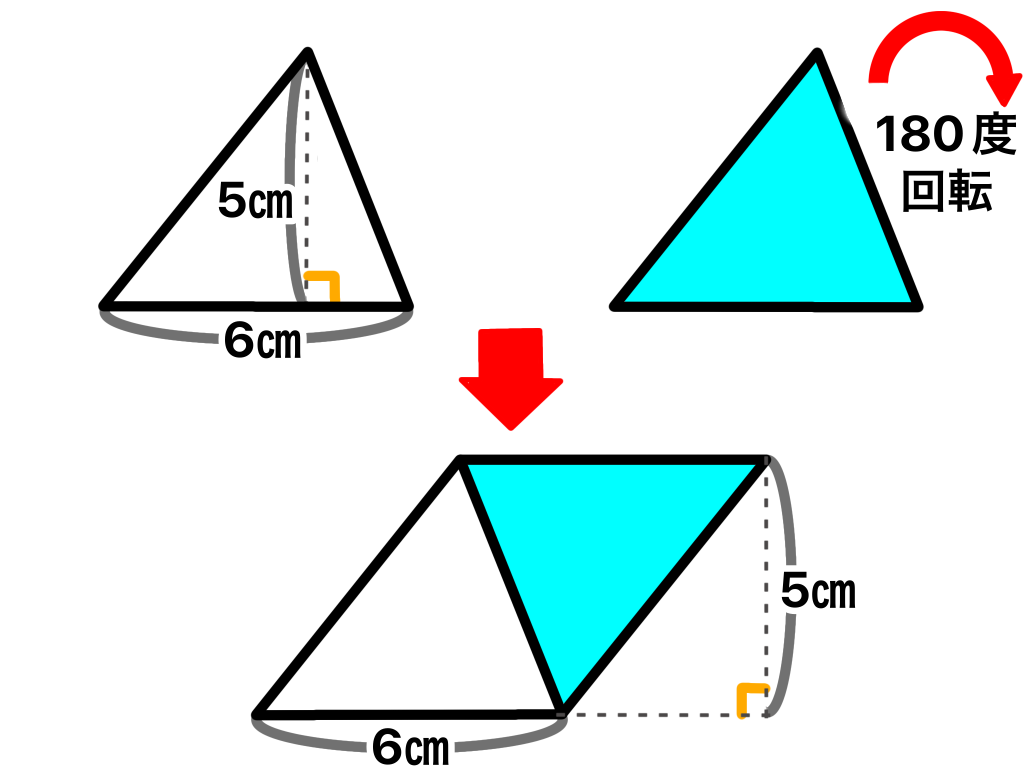
同じ形、大きさの三角形をもう一つ用意します。
その三角形を180°回転させ、元の三角形に合わせます。
(三角形同士を合わせるときは同じ辺同士を合わせます)
すると一つの平行四辺形ができます。
平行四辺形は底辺×高さで求められるので
この同じ三角形二つを合わせた面積は
6(底辺)×5(高さ)=30[㎠]
となります。
ここから三角形1つ分の面積を求めたいので
この平行四辺形を1/2にすると求めたい三角形の面積を求めることができます。
なので三角形の面積の求め方は
底辺×高さ÷2
で求めれることがわかります( ̄▽ ̄)
多角形の面積
多角形の定義の説明は難しいので省かせてもらいます( ̄▽ ̄;)
大抵のカクカクしてる図形は多角形です( ̄▽ ̄)
多角形の面積は計算できる三角形、四角形に分解して求めます。
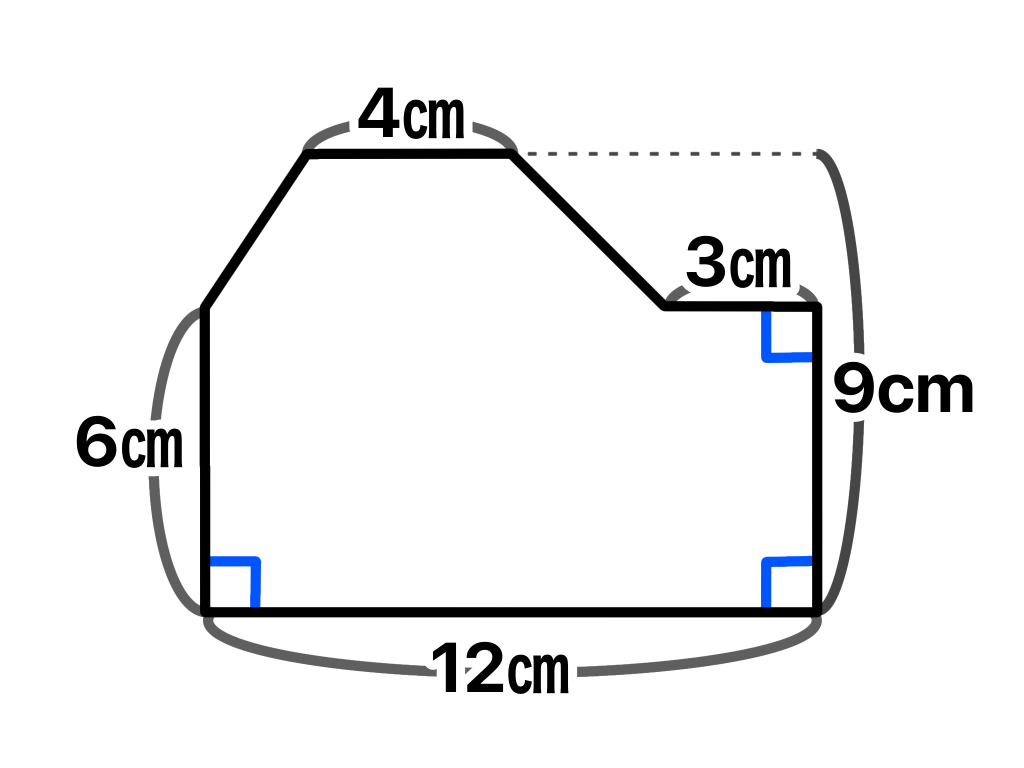
例えばこの図形は長方形と台形に分解して計算することができます。
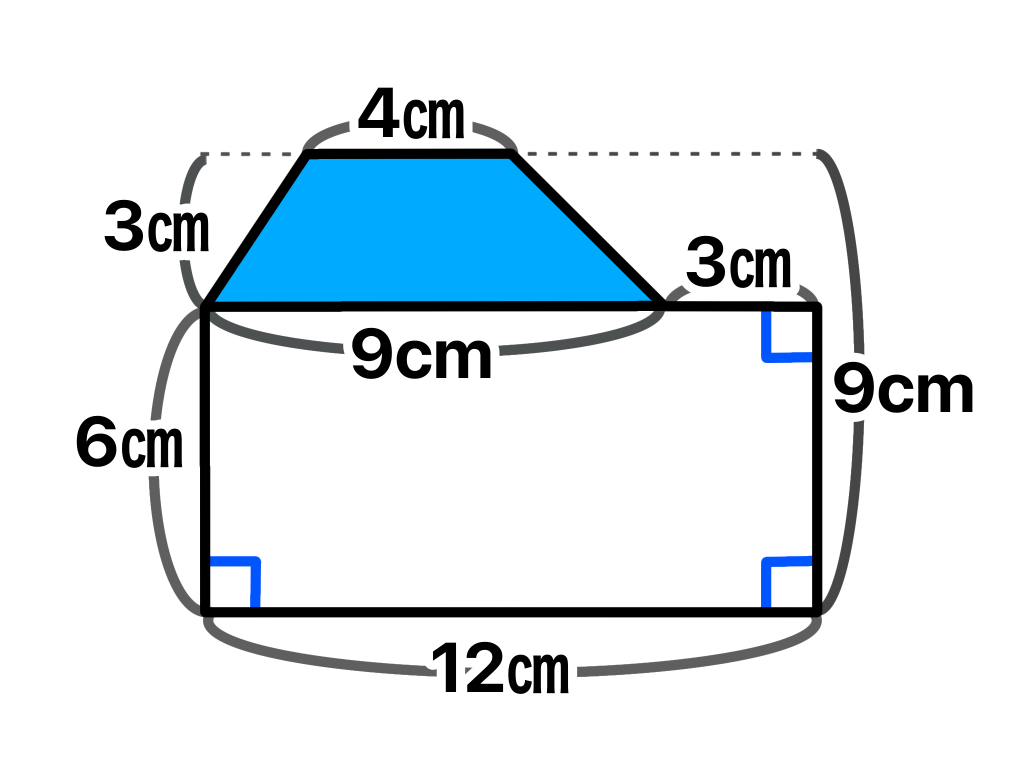
上のように線を引くと台形と長方形ができます。
台形の面積の求め方はこちらから( ̄▽ ̄)
与えられている長さから台形の下底の長さを求めることができます。
台形部分の面積
(4+9)×3÷2=19.5[㎠]
長方形部分の面積
12×6=72[㎠]
求めたこれらの面積を合わせて
19.5+72=91.5[㎠]
よってこの図形の面積は
91.5㎠となります(*^_^*)
もう1つ多角形の面積を求めてみます。
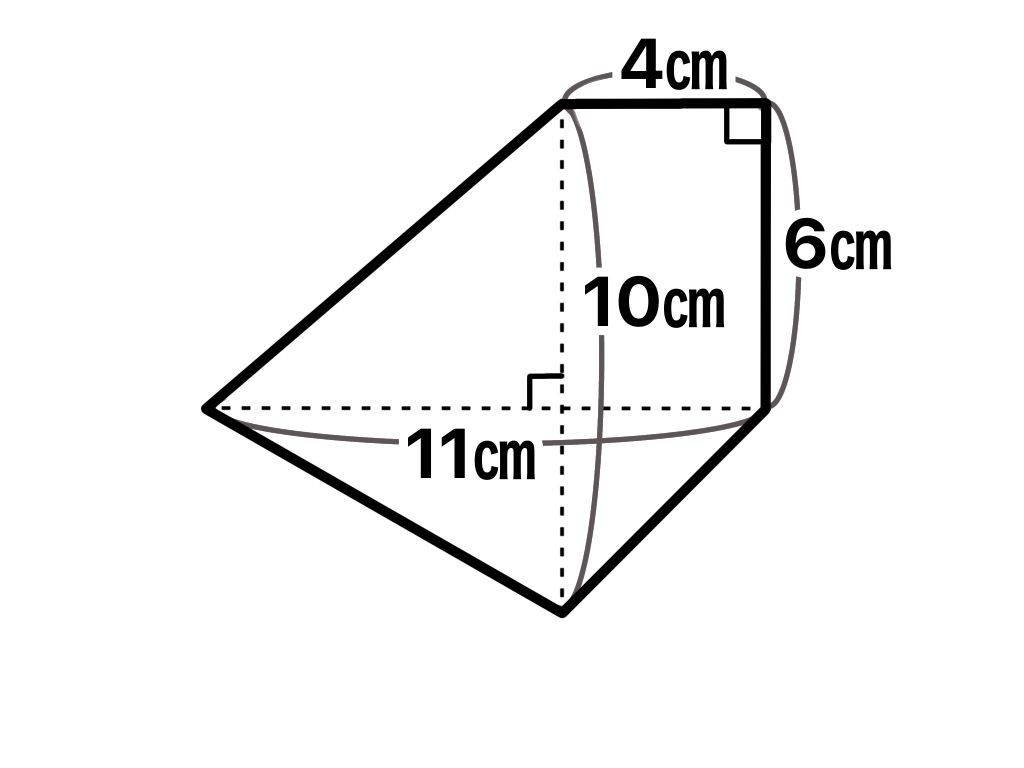
この図形もさっきの図形と同様、線を引き求めやすい図形に分解します。
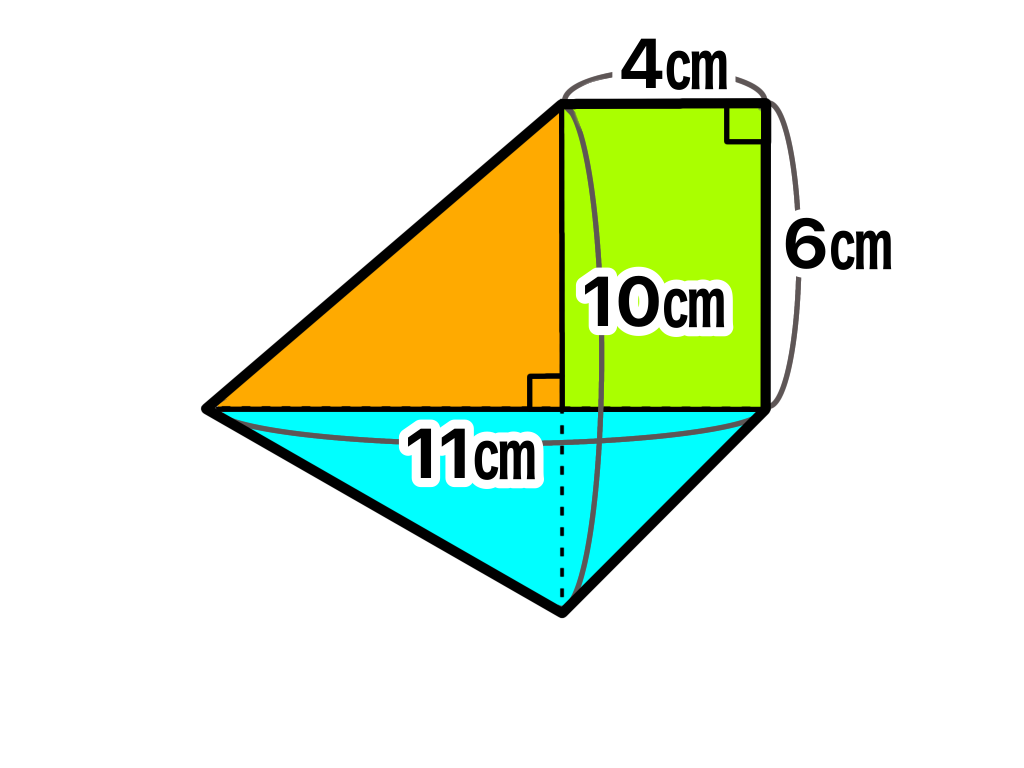
このように線を引くと長方形と2つの三角形に分解することができます。
それでは面積を求めていきます( ̄▽ ̄)
長方形
4×6=24
黄・三角形
(底辺)11-4=7
7×6÷2=21
青・三角形
(高さ)10-6=4
11×4÷2=22
24+21+22=67
この多角形の面積は67㎠となります( ̄▽ ̄)
以上が三角形、多角形の面積でした( ̄▽ ̄)
三角形と四角形の面積をしっかり覚えてく必要がありますね(*^_^*)
それでは復習お疲れ様でした( ̄▽ ̄)/

