こんにちは
こいパパです( ̄▽ ̄)
今回は面積についてや、四角形の面積の求め方についてやり直し学習していこうと思います!
面積とは
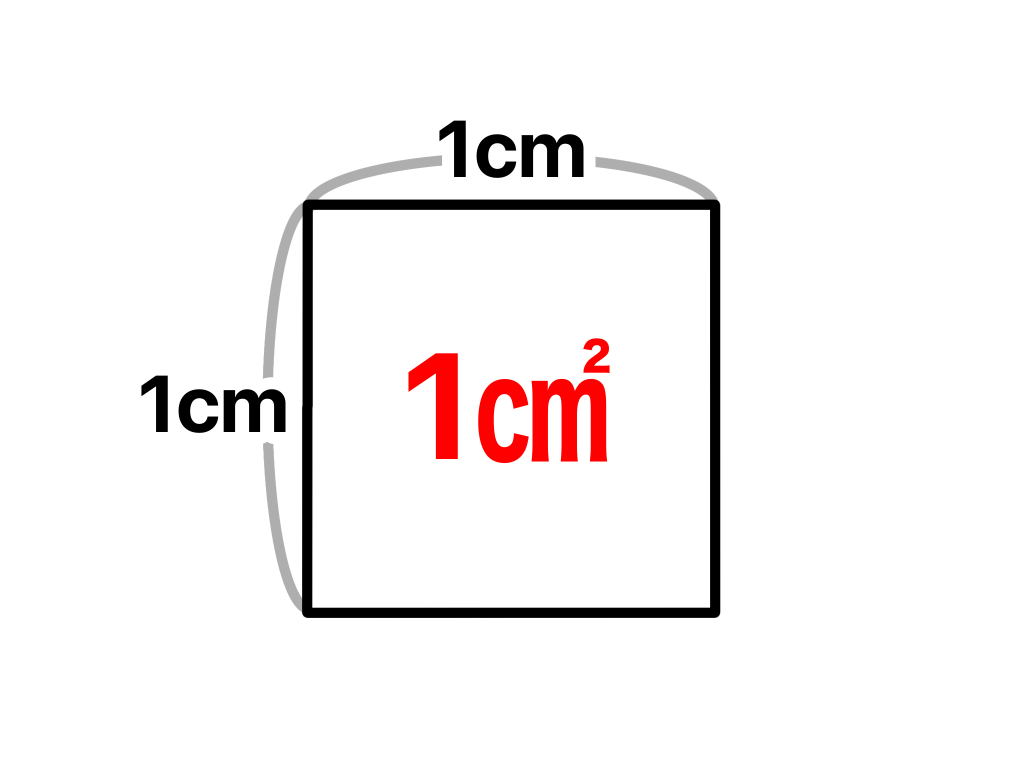
1㎝×1㎝の広さを1㎠(平方センチメートル)という単位で表します(*^_^*)
次はもう少し大きい面積についてみていきます。
縦、横4㎝の正方形で考えていきます( ̄▽ ̄)
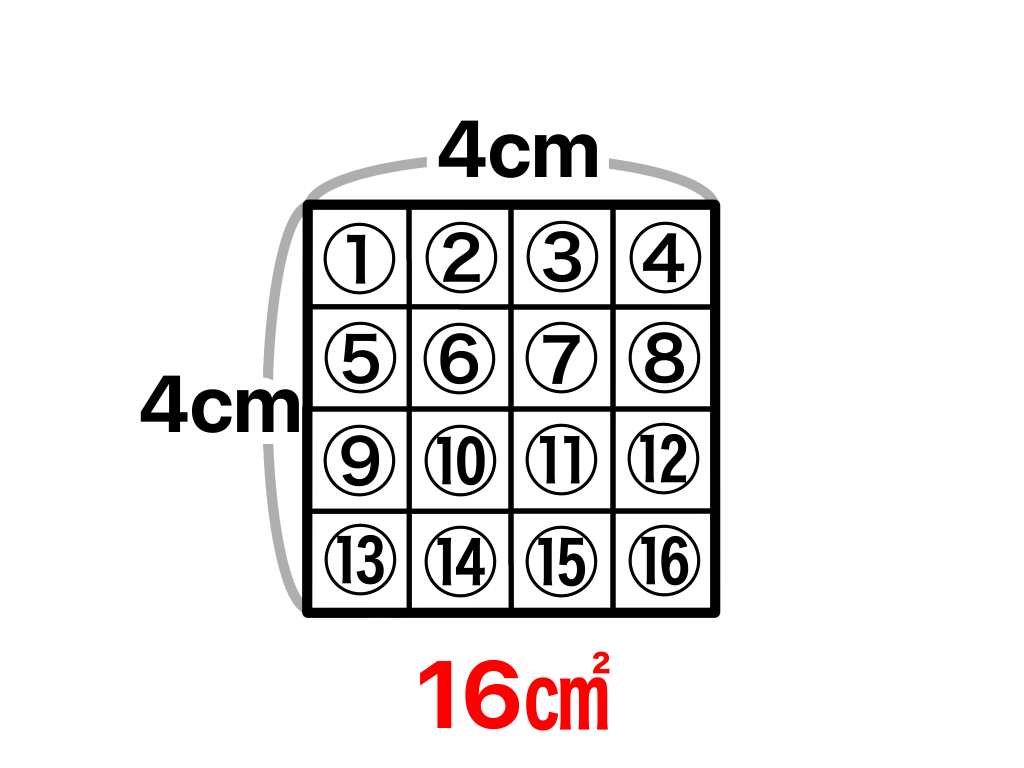
上の図から縦、横4㎝の正方形の面積は1㎠16個分なので16㎠となります。
計算式では4×4=16で表せます。
四角形の面積
四角形の面積を求める計算の方法は異なります( ̄▽ ̄)
正方形
長方形
平行四辺形
台形
ひし形
これらの四角形の面積の求め方を見ていきたいと思います( ̄▽ ̄)
正方形・長方形
正方形と長方形は面積の求め方が同じです( ̄▽ ̄)
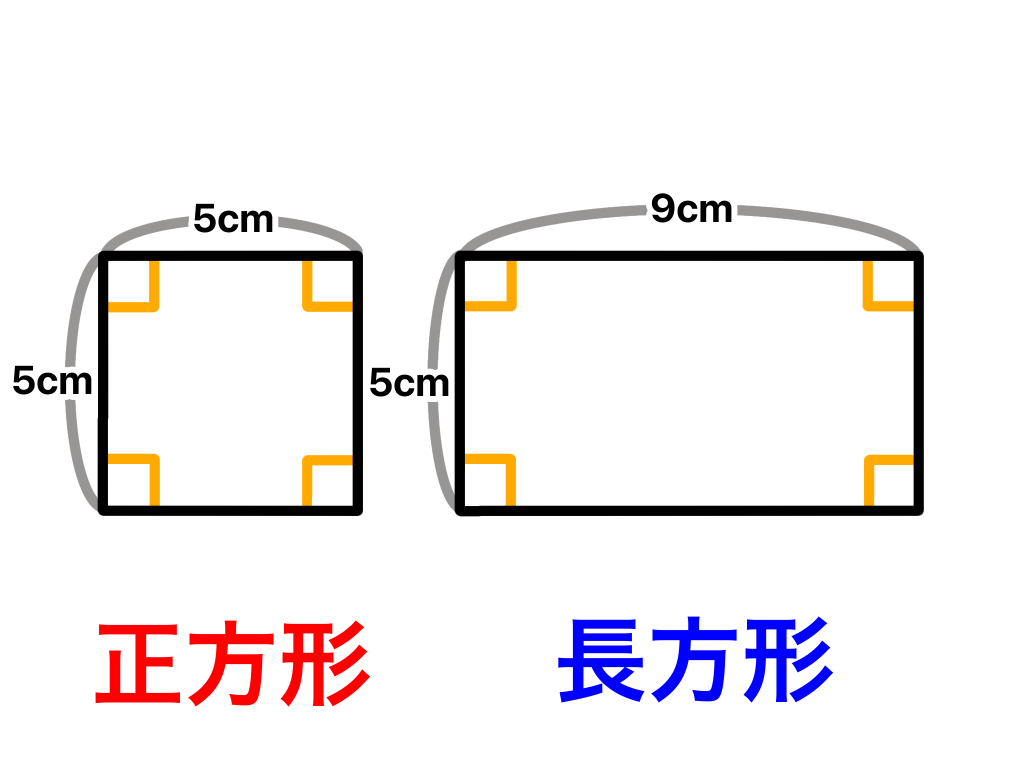
正方形とは4つの角が90度で縦、横の長さが同じ四角形です( ̄▽ ̄)
長方形は正方形と同じく4つの角が90度ですが縦、横の長さが異なった四角形です(*^▽^*)
面積の求めた方は
縦の長さ×横の長さ
で求めることができます( ̄▽ ̄)
上の図の正方形と長方形の面積を求めてみたいと思います。
正方形
縦5㎝,横5㎝なので
5×5=25
正方形の面積は25㎠です(*^_^*)
長方形
縦5㎝,横9㎝なので
5×9=45
長方形の面積は45㎠です(*^▽^*)
正方形と長方形の面積の求め方が他の四角形の面積を求める時のベースになります( ̄▽ ̄)
平行四辺形
平行四辺形とは、向かい合う辺同士が平行である四角形です( ̄▽ ̄)
平行四辺形の向かい合う辺は同じ長さになります。
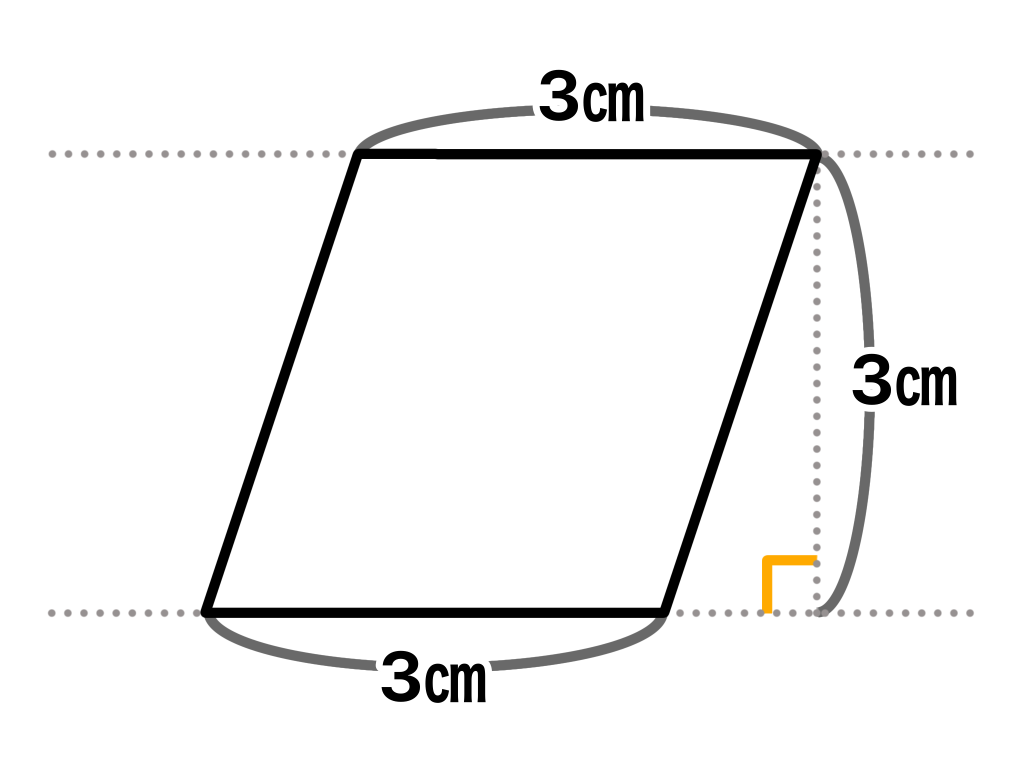
平行四辺形の下の辺を底辺と呼びます。
上の図の場合底辺は3㎝となります。
平行四辺形の面積の求め方は
底辺×高さ
で求めることができます( ̄▽ ̄)
高さは底辺から上の辺までの長さのことをいいます。
高さは底辺に対して垂直に計ります。
ではどうして底辺×高さで表せれるのか考えてみましょう(*^_^*)
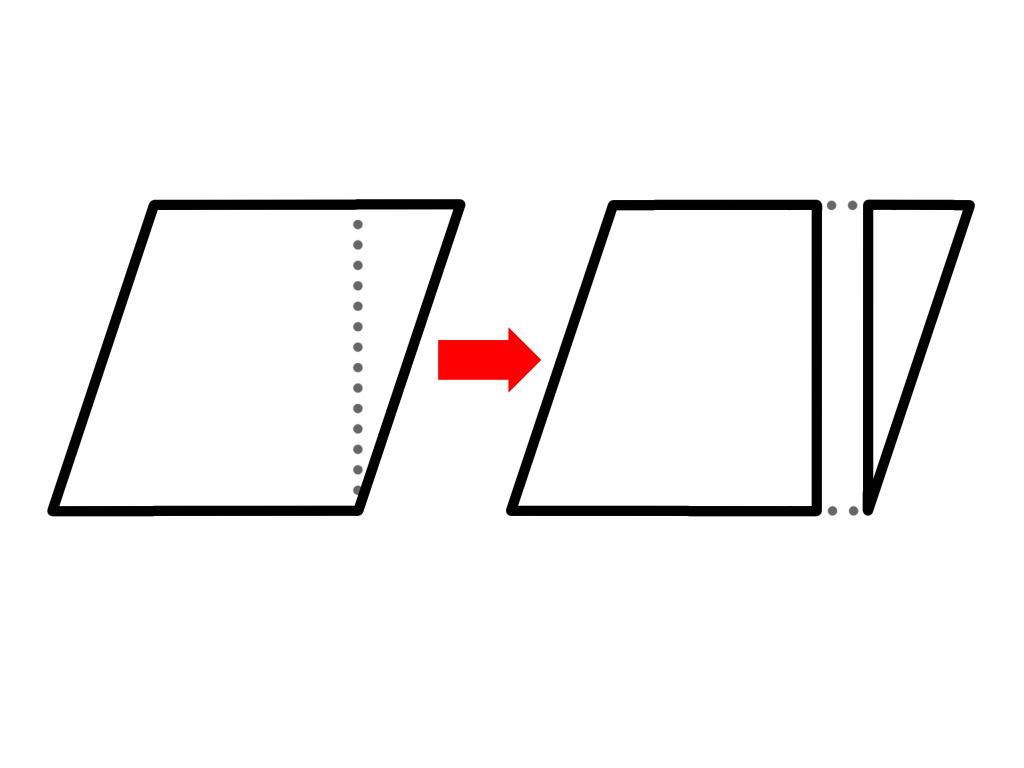
上の図のように底辺の端から垂直に切り離します。
すると直角三角形ができます( ̄▽ ̄)
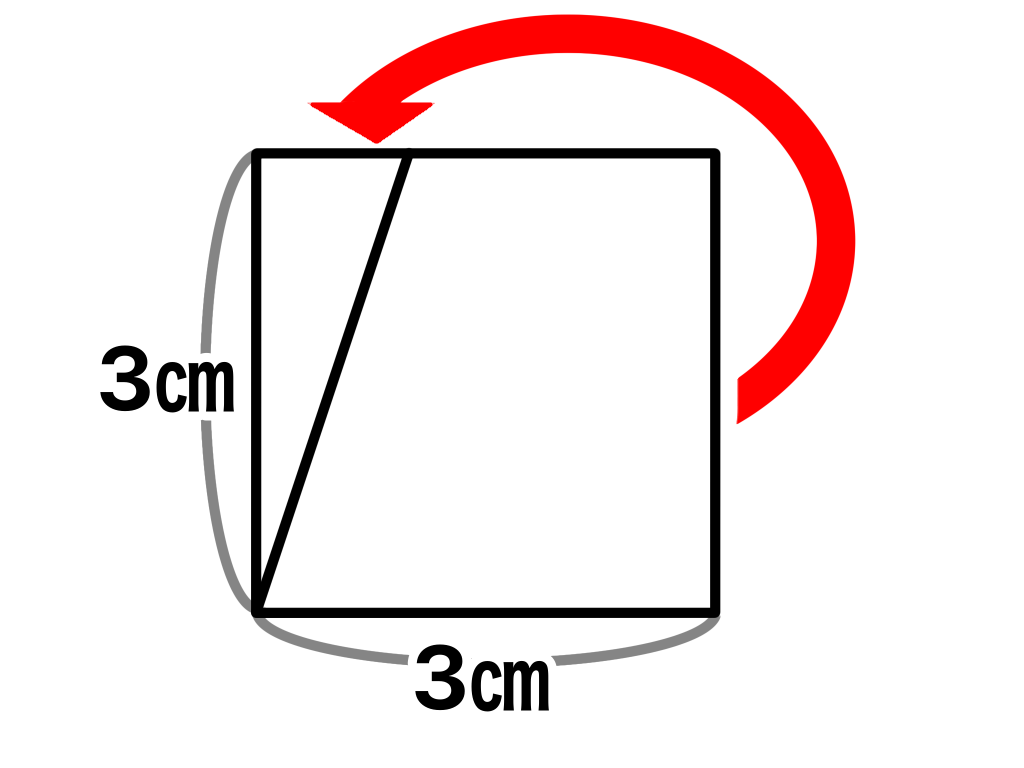
切り離した直角三角形を上の図のようにもってくると正方形または長方形ができます(*^▽^*)
このことから平行四辺形は底辺×高さで面積を求めれることがわかります( ̄▽ ̄)
公式(面積の計算式)の意味を理解できると覚えやすいですね( ̄▽ ̄)
台形
台形とは平行な辺が1組ある四角形です( ̄▽ ̄)
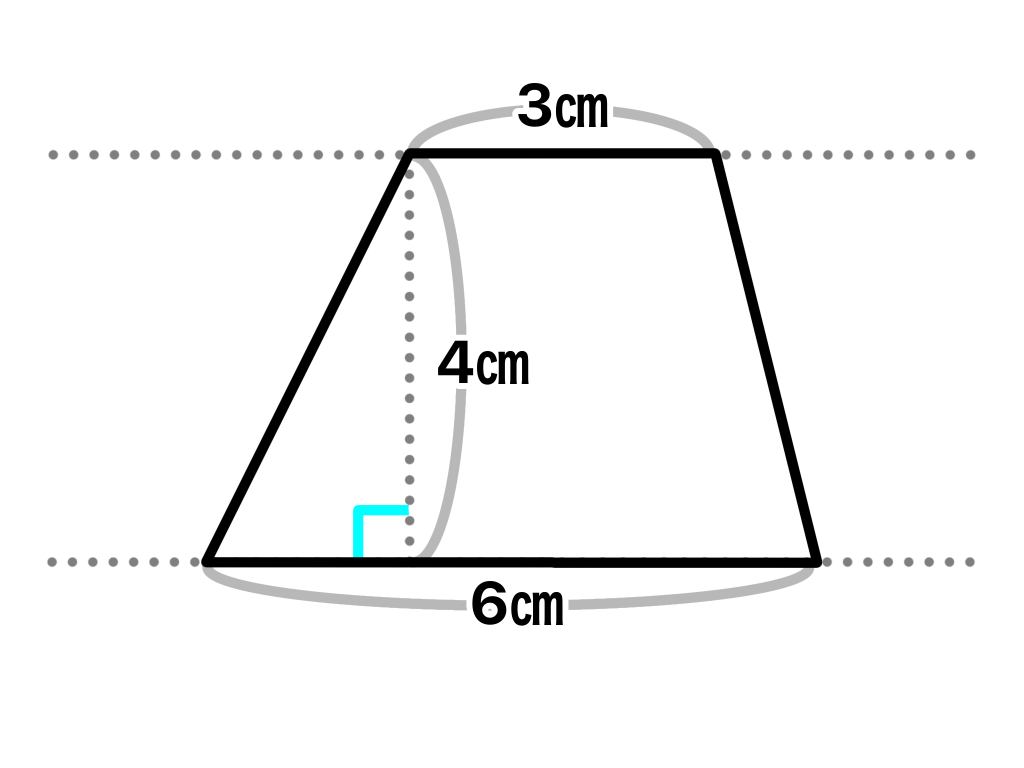
平行四辺形とは違い平行な辺は1組なので辺の長さはそれぞれ異なることがあります。
台形の平行な辺のうち上の辺を上底、下の辺を下底といいます。
上の図の上底は3㎝、下底は6㎝となります。
台形の面積の求め方は
(上底+下底)×高さ÷2
で求めることができます( ̄▽ ̄)
ではどうしてこのような公式なのか考えていきましょう(*^_^*)
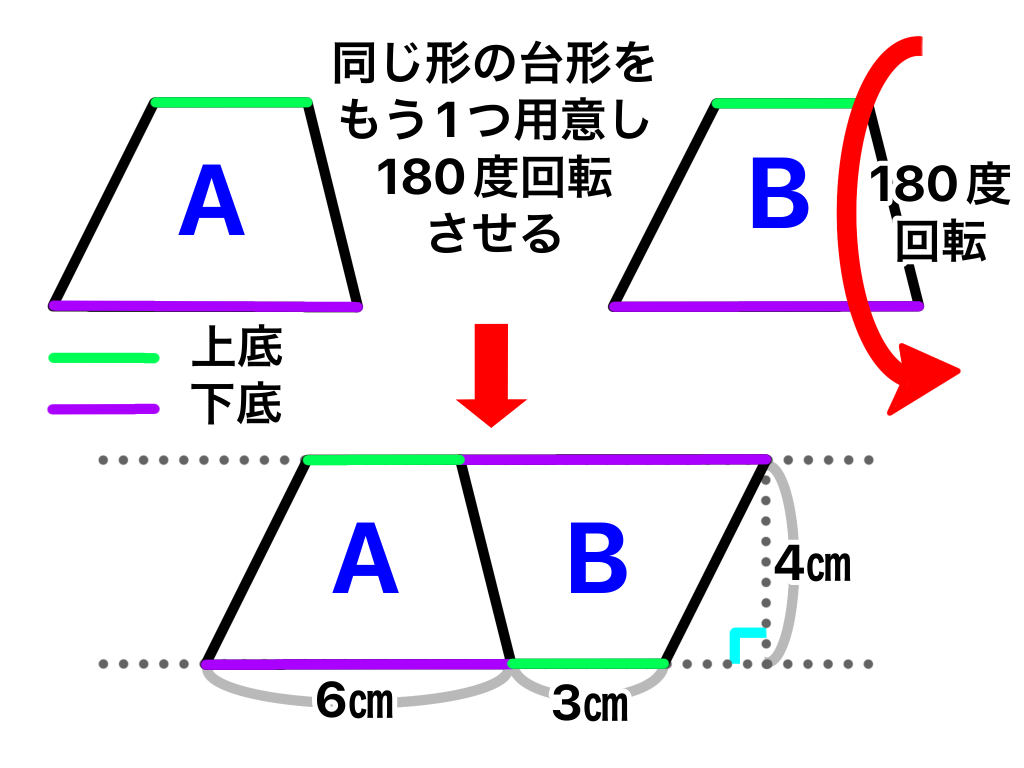
1つの図にまとめようと思ったらごちゃごちゃしていまいました( ̄▽ ̄;)
上の図のように同じ形、大きさの台形をもう一つ用意し、その台形を180度回転させます。
そして2つの台形を組み合わせて一つの四角形にします。
するとこの四角形は平行四辺形になります。
平行四辺形の面積を求める公式は
底辺×高さです( ̄▽ ̄)
上の図をみてもらうとわかるように底辺が上底+下底になることがわかります。
そしてこの平行四辺形は求めたい台形2つ分の面積なので、
2で割った面積が台形の面積となります。
よって台形の面積を求める公式は
(上底+下底)×高さ÷2
ということになります( ̄▽ ̄)
では上の図の面積を求めてみます。
(3+6)×4÷2=18
よってこの台形の面積は18㎠となります。
ひし形
ひし形とは4つの辺の長さが全て等しい(同じ)四角形のことです。
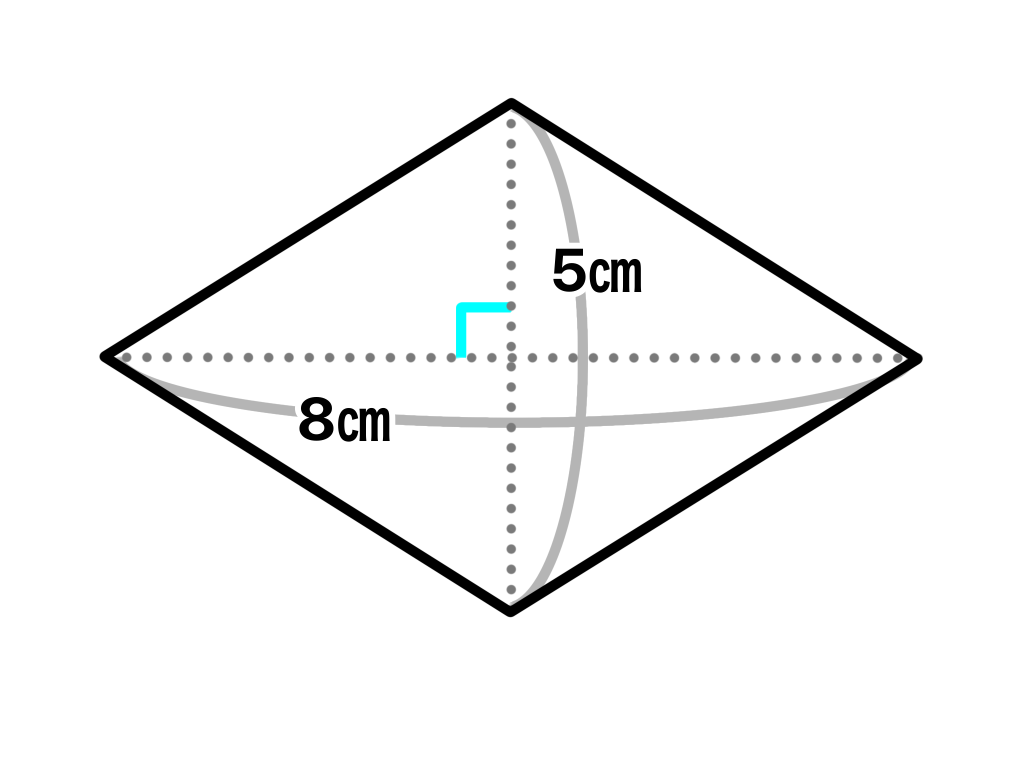
ひし形の面積を求めるには
対角線×対角線÷2
で求めることができます( ̄▽ ̄)
対角線とは向かい合う点と点を線で結んだものです(*^_^*)
それでは何故この公式で求めることができるか考えていきたいと思います。
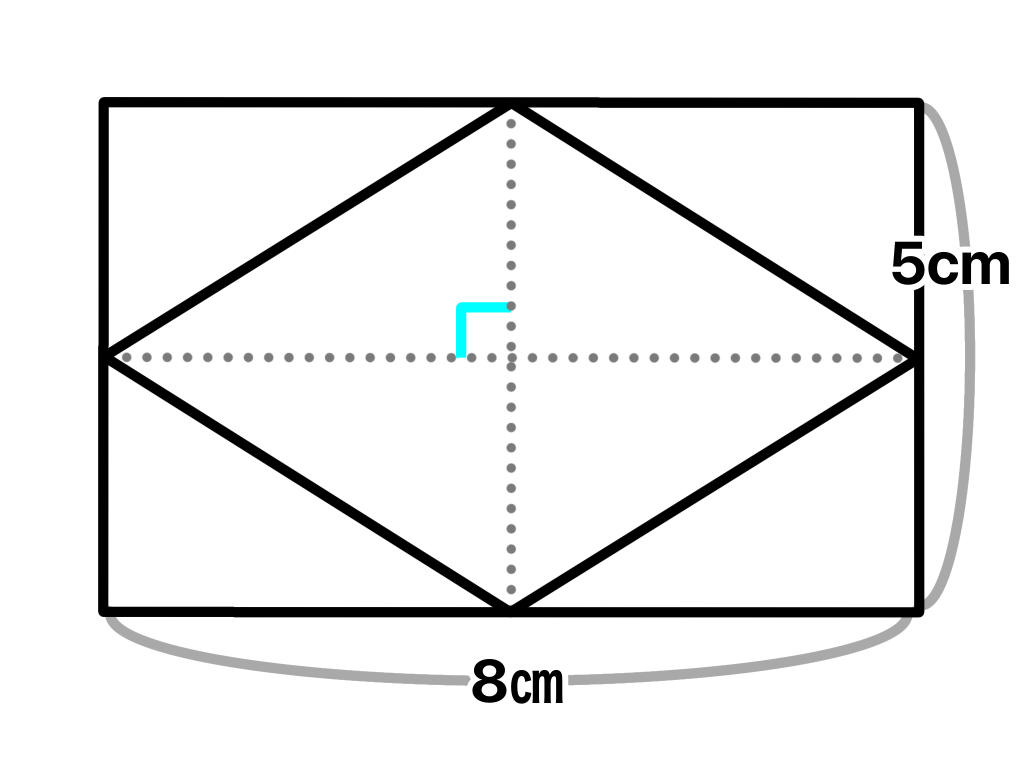
対角線と対角線を掛けることによって上の図のようにひし形を囲む長方形の面積を求めることができます(*^_^*)
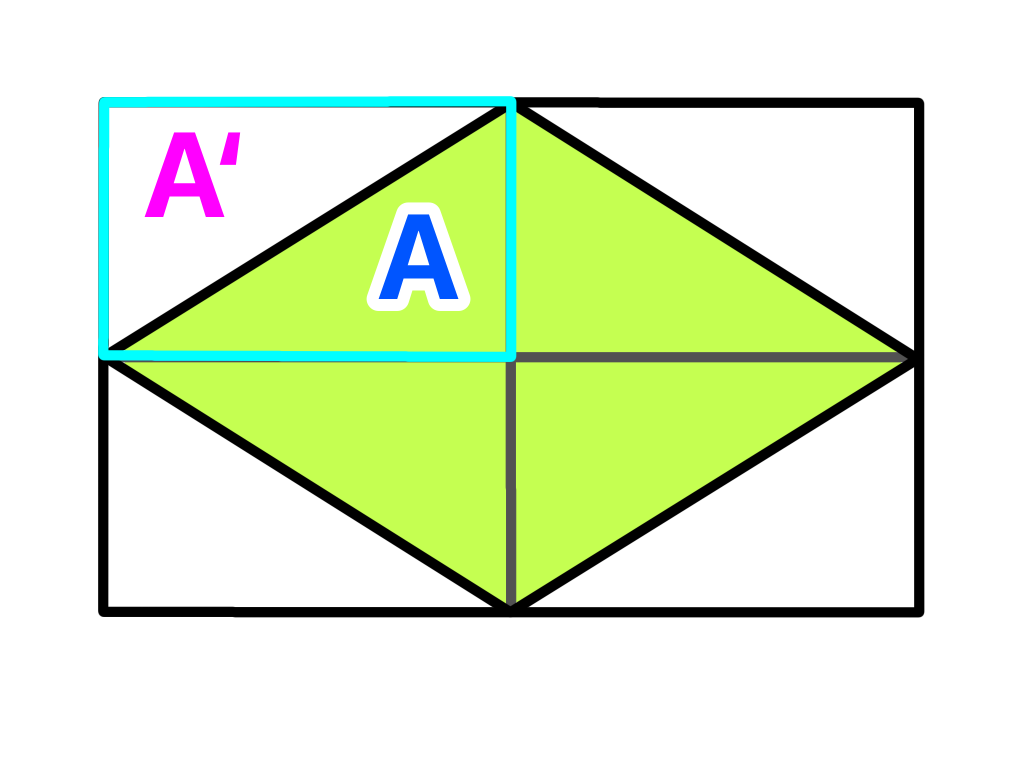
この図を長方形の内側のひし形とそれ以外とで色分けしてみます(*^_^*)
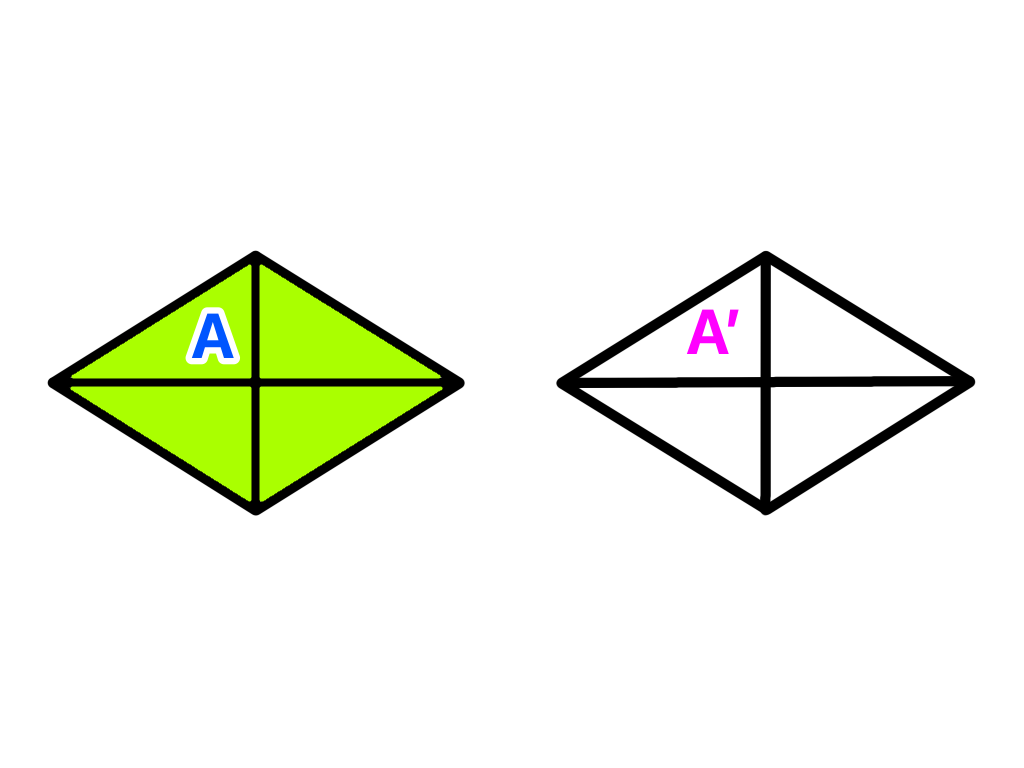
この外側の4つの三角形を合わせると同じ形のひし形がもうひとつできます( ̄▽ ̄)
つまり÷2することでひし形1つ分の面積を求めることができます。
よって対角線×対角線÷2することでひし形の面積を求めることができます(*^▽^*)
以上が四角形の面積でした(*^▽^*)
公式を暗記するのも大事ですが
何故そうなるのかを考えるとより一層覚えやすいですね(*^_^*)
それでは復習お疲れさまでした!
こいパパでした( ̄▽ ̄)/


