【小学校の算数⑫】拡大図・縮図・合同図

こんにちは！
こいパパです(￣▽￣)

今回は拡大・縮小・合同の図形についてやり直し学習していこうと思います(*^_^*)

拡大図

拡大図とは図の縦、横など長さの比を変えずにを拡大したものです(*^_^*)

以下の図は長方形の図を３倍に拡大したものです(￣▽￣)

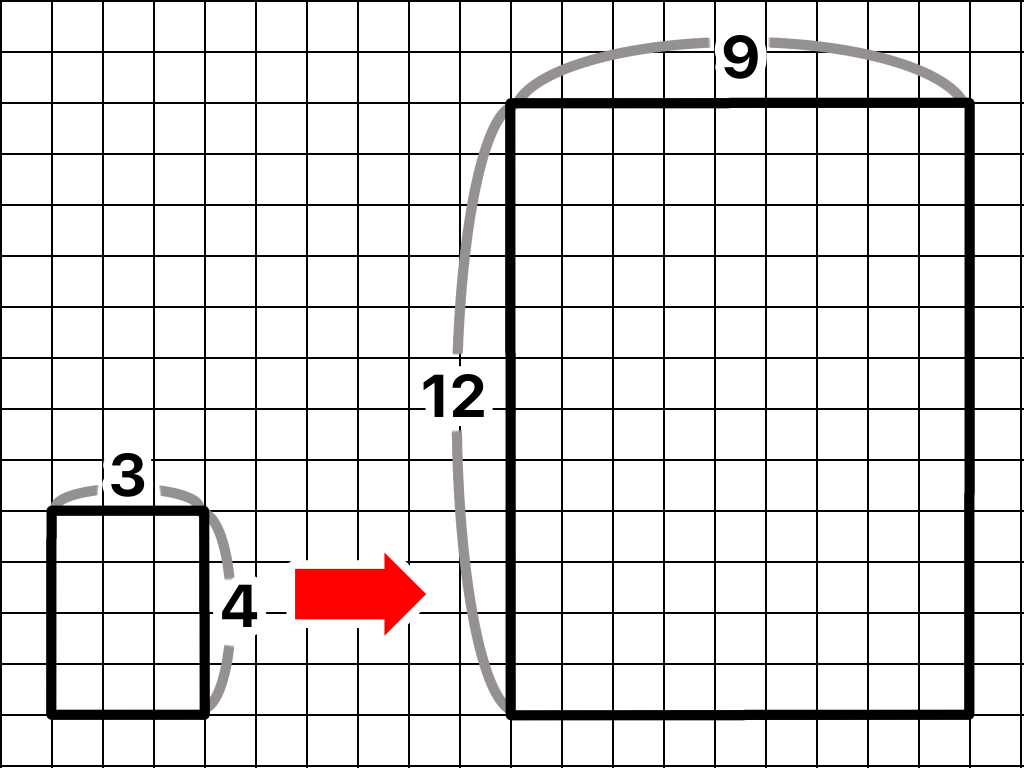
図を見てわかるように縦、横の長さがともに３倍になり縦、横の比は変わっていません。

地図アプリをイメージすると分かりやすいですね(￣▽￣)
拡大、縮小しても縦、横の比率が変わらず大きくなったり小さくなったりしますよね(*^_^*)
ちなみに大きくした割合のことを倍率といいます(*^▽^*)

縮図は拡大図とは反対に図を縮小した図です(￣▽￣)

下の図は三角形を１／２に縮小した縮図になります(*^_^*)

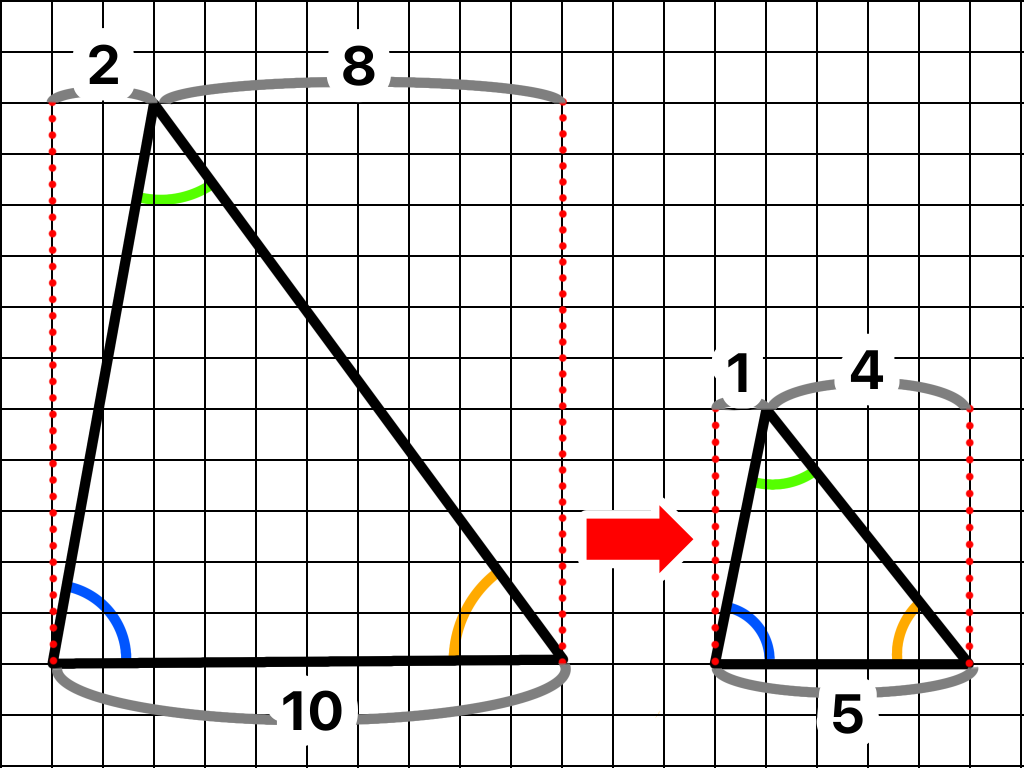
三角形を拡大、縮小しても三角形の内角は変わりません(*^▽^*)

縮めた割合を縮尺といいます(*^▽^*)

合同とは２つの図形がぴったり重なり合うことをいいます。
ある２つの図形が同じ形、大きさのとき２つの図形は合同ということになります。

下の図にA～Fまでの三角形と四角形の図形があります。
次のうち合同の図形（全く同じな図形）の組み合わせはどれでしょう(￣▽￣)

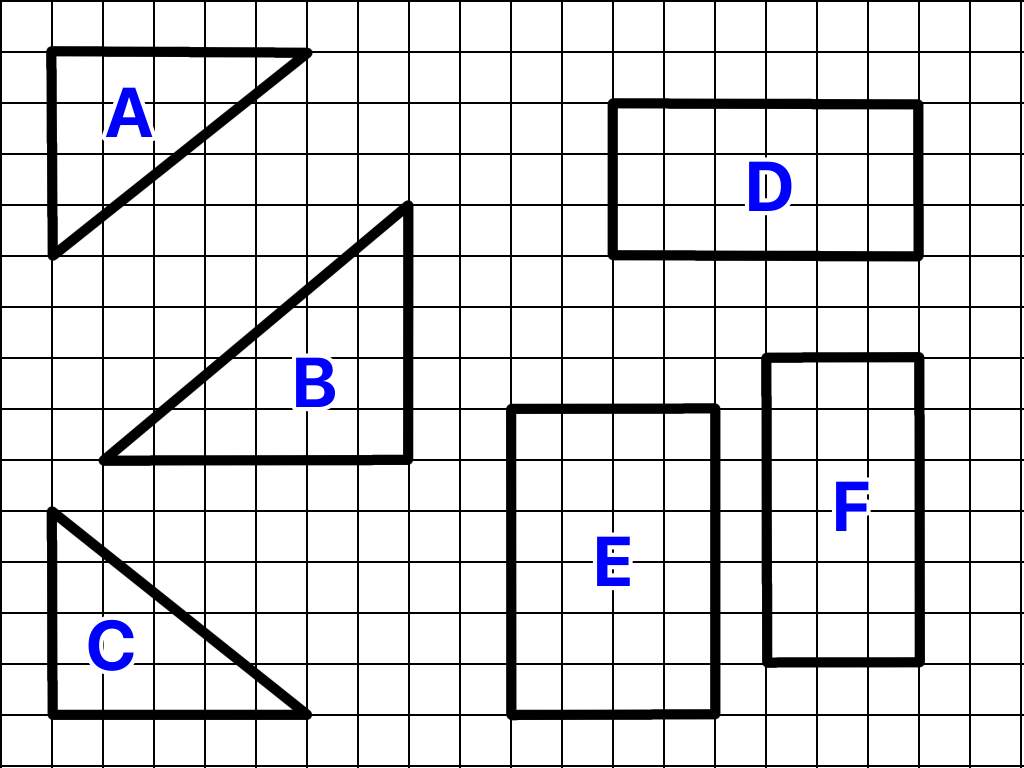
まず簡単な四角形から見ていきましょう(￣▽￣)
図の四角形はど３つとも長方形です。

長方形同士がが合同かは縦と横の長さが同じかで決まります。
それでは縦と横の長さが同じ長方形を探していきます(*^_^*)

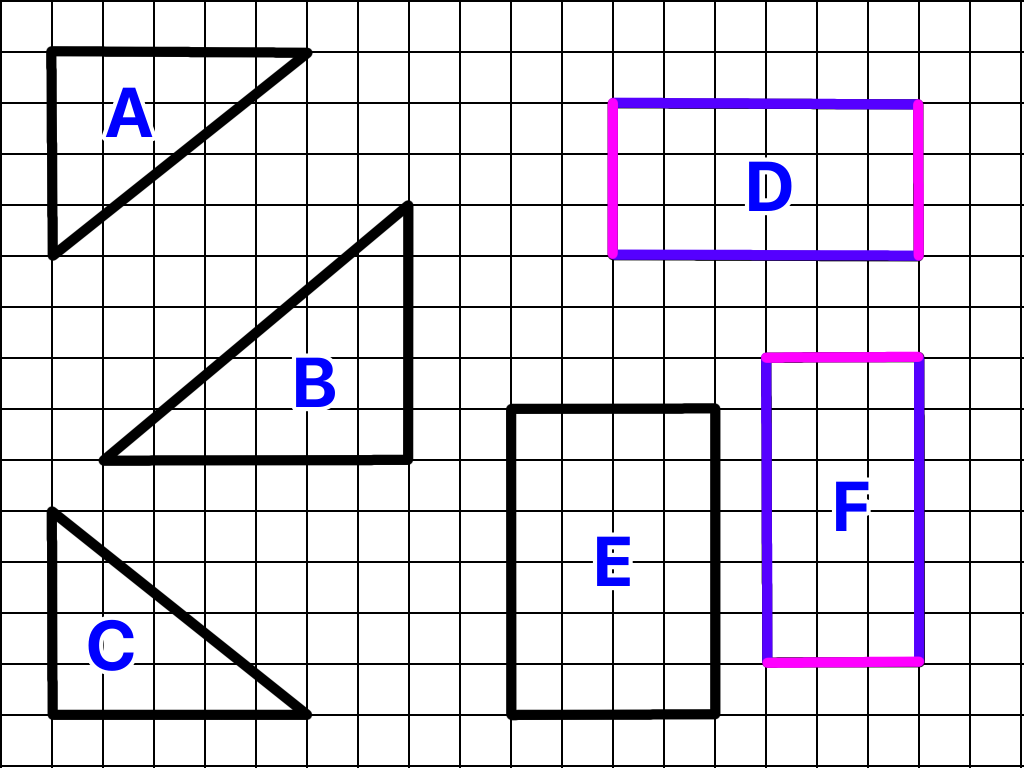
同じ長さの線を色分けしてみました(*^_^*)

紫の線は３マス
青の線は６マス

よってDとFの長方形は大きさが同じであり、合同ということになります(￣▽￣)

次は合同な三角形を探していきましょう(*^_^*)

三角形の合同は小学校ではやらないみたいですね(￣▽￣;)
なのでさらっとやってしましたいと思います(￣▽￣)

三角形の合同条件は３つあります。

上の図の三角形は直角三角形なので一つの角が９０度です。
その周りの２つの辺の長さが同じなら合同となります。

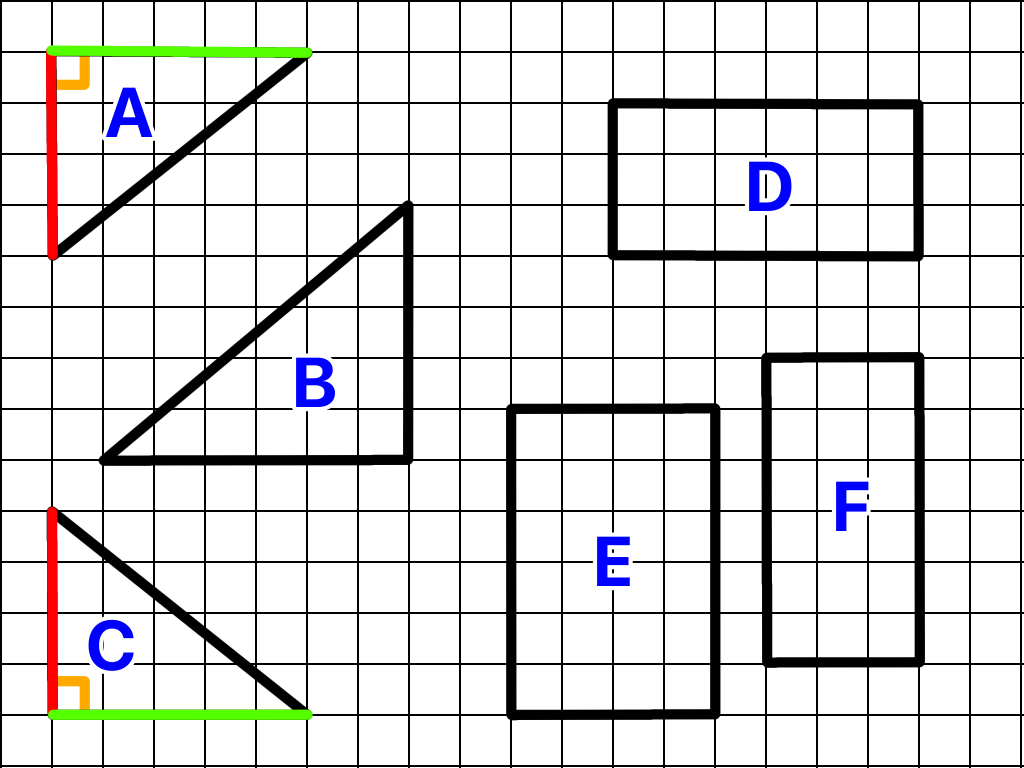
上の図は直角三角形で同じ長さどうしの辺を色分けした図です(*^_^*)

赤色の辺は４マス
黄緑色の辺は５マス
２辺の間の角は直角三角形なので９０度

これにより三角形の合同条件である

２組の辺の長さとその間の角度がそれぞれ等しい

の条件に当てはまるのでAとCの三角形は同じ大きさ、形である合同となります(￣▽￣)

直角三角形は三角形の合同条件とは別に合同条件があります(￣▽￣)
記載しておきますが今回は説明は省きたいと思います(*^▽^*)

・斜辺と１つの鋭角がそれぞれ等しい
・斜辺と他の１辺がそれぞれ等しい

の２つの合同条件があります(￣▽￣)

以上！

拡大図と縮図、合同でした(*^▽^*)

小学校で習うことを調べながら学び直しをしているのですが…
これ小学校でならったっけ！？

って思うことが多いですねー(￣▽￣)

まぁ目的の範囲外でも自分の為になるしいっか～
くらいに思って復習しています(￣▽￣)笑

それでは復習お疲れさまでした！

こいパパでした(￣▽￣)／