こんにちは
こいパパです( ̄▽ ̄)
今回も大人になってからのやり直し学習をしていこうと思います!
並び方
並び方とは
並び方とは複数のものを並び替えた時に、何通りの並べ方ができるのかというものです。
例えば3人の人がいます。
この3人が一列に並ぶときに何通りの並び方ができるでしょうか( ̄▽ ̄)?
3人を分かりやすくA,B,Cと置き換えます。
まずAが先頭にくる並び方を考えます。
Aが先頭にきた時後ろにくるB,Cの並び方を考えます。
A・B・C
A・C・B
Aが先頭にくる時の並び方は2通りあることがわかります。
以上のことより、BとCがそれぞれ先頭にくる時も2通りずつあることがわかります。
なので2×3=6通りの並び方ができることがわかります。
\詳しく解説/
A,B,Cの誰が先頭にきても後の並び方は2通りになります。
Aが先頭ならばB,CかC,Bしかないですからね( ̄▽ ̄)
これはBやCが先頭にきても残りの並び方は一緒の2通りです。
なので
2(2通りずつ)×3(3人それぞれが先頭にくるとき)
という考え方になります。
計算がわかりにくいときは全部のパターンを書き出してしまえばいいです( ̄▽ ̄)!
[A・B・C],[A・C・B]
[B,A,C],[B,C,A]
[C,A,B],[C,B,A]
全部で6通りです(*^_^*)
樹形図
樹形図は並び方を分かりやすく図に表したものです。
次の図は1,2,3,4の4つの数字の並び方で、1から始まる並び方の樹形図です( ̄▽ ̄)
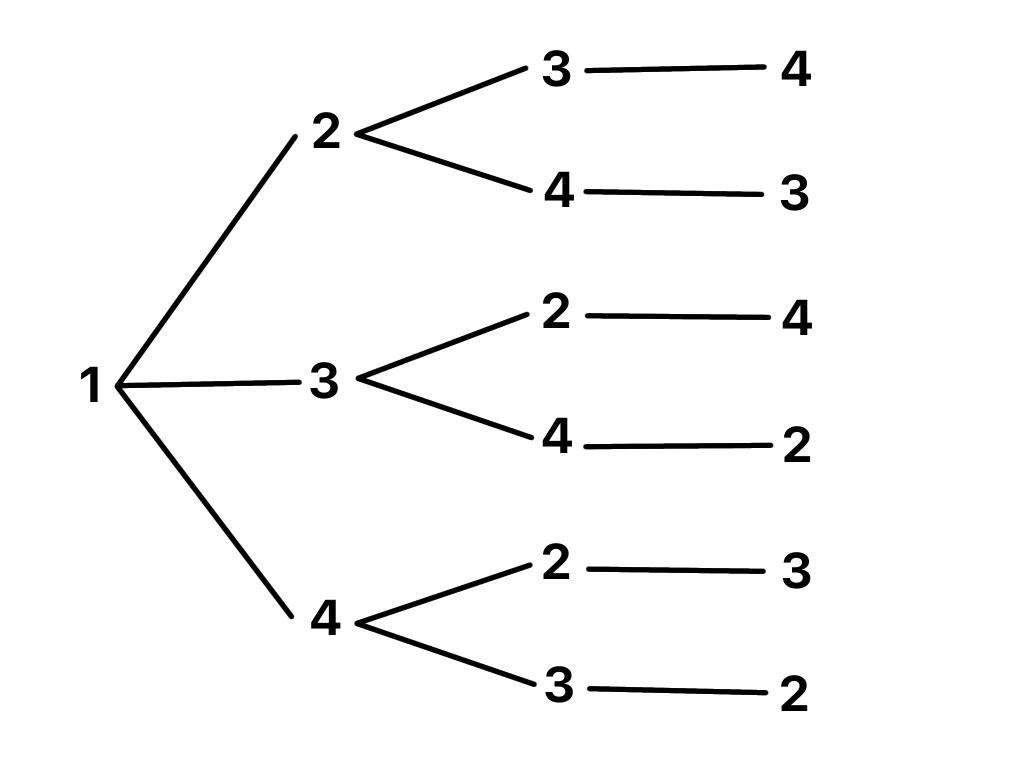
上の樹形図より1から始まる並び方は6通りあることがわかります。
このように樹形図に表すことで分かりやすくなりますね(*^_^*)
2~4から始まる並び方も上の樹形図と同様に考えることができるので、それぞれ6通りあることがいえます。
なので6×4=24
1,2,3,4の4つの数字の並び方は全部で24通りあることがわかります(*^_^*)
【例題】
コインを4回連続で投げた時の表と裏の出方は全部で何通りありますか?
\ポイント/
コインは1回投げるごとに表、裏の2通りの出方があります。
1回目が表の時の樹形図が下の図になります。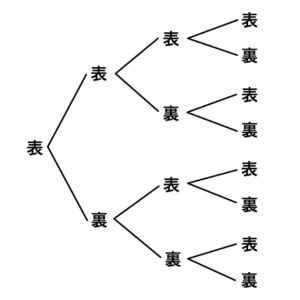 1回目が表の時コインの出方は8通りあることがわかります。
1回目が表の時コインの出方は8通りあることがわかります。
1回目が表と裏の2通りですので
8×2=16
コインを4回連続で投げた時のコインの表、裏の出方は16通りあることがわかります。
計算で算出することもできます( ̄▽ ̄)
コインは1回で2通り。
それを4回繰り返すので
2×2×2×2=16
組み合わせ
組み合わせとは複数あるものの組み合わせが何通りあるのか、とうものです。
例えばA,B,C,Dの4人が腕相撲で総当たり戦をするとき、全部で何戦行うでしょうか?
[A,A]など同じもの同士や[A,B],[B,A]など同じ組み合わせなどは含まないようにしないといけません( ̄▽ ̄)
全部書き出してみると
[A,B][A,C][A,D][B,C][B,D][C,D]
全部で6戦行うことがわかります( ̄▽ ̄)
ではこれを計算で出してみましょう!
まずAが何戦するかを考えます。
AはB,C,Dの3戦行います。
つまり
4(人)-1(A,Aは含まないので)
=3(戦)
並び方と同じ考え方で計算します。
3(戦)×4(人)=12
そしてこの中には[A,B][B,A]も含まれています。
これは全部の半分を占めます。
説明すると
[B,A][B,C][B,D]
[C,A][C,B][C,D]
[D,A][D,B][D,C]
全部で12通り。
同じ組み合わせを除きます。
[A,B][A,C][A,D]このように同じ組み合わせが半分を占めるので
12÷2=6
となります( ̄▽ ̄)
個人的には計算するより書き出した方が早い気がします( ̄▽ ̄)
以上が並び方と組み合わせでした( ̄▽ ̄)!
ぼく的に「こんなのあったな~」くらいの感じでしたね(*^▽^*)
ほぼほぼ忘れてました( ̄▽ ̄)
復習お疲れさまでした!
こいパパです( ̄▽ ̄)/


