こんにちは!
こいパパです( ̄▽ ̄)
今回は量を比較する比
比例、反比例についてやり直し学習していこうと思います(*^_^*)
比
比とは
比とは、量の割合を比較したものです。
2つの比を表すときは〇:△と表します。
例えば小麦粉の重さ500gと水の重さ300gの比を表すときは500:300と表します。
比を表すときは簡単な比で表します。
簡単な比とは〇:△の両方に同じ数を割ったりしてできる分かりやすい比のことです。
500:300の簡単な比を考えていきます。
まず500と300の最大公約数を求めてみましょう。
500と300の最大公約数は100です。
比の両方を100で割ります。
100で割ると比は5:3となります。
500:300と5:3は比は同じなので
500:300=5:3という式で表すこともできます(*^▽^*)
比についてイメージしにくいときはこう考えましょう(*^_^*)
1人前のパスタは100g、3人前は3倍のパスタ300g。
これを比の式で表すと…
1:100=3:300となります。
何人前作るとしても1人前が100gという比は変わらないということです( ̄▽ ̄)
比の値
比の値はわり算で求められます( ̄▽ ̄)
A:Bの比の値は
$$A÷B=\frac{A}{B}$$
では比についての問題をやってみましょう(*^_^*)
【例題1】
21:56の比の値を求めてください。
【求め方】
$$21÷56=\frac{21}{56}=\frac{3}{8}$$
比の値を求めるときは分数まででOK!( ̄▽ ̄)
【例題2】
次の式のxの値を求めてください。
9:x=15:25
【求め方】
xにあてはまる値を考える問題ですね。
=で結ばれている比は同じになります。
例えば、
x:y=3x:3y
のようにxとyに同じ数を掛けた倍数になります。
では問題の
9:x=15:25
について考えていきます。
まず式の右側を簡単な比にします。
15と25は5の倍数なので5で割ります。
15(÷5):25(÷5)=3:5
9:x=3:5となり計算しやすくなります。
式の左側の比をどうしを比べると
式の左の比は右の比の3倍であることがわかります。
9:x=3:5
3×3=9
5×3=x
x=15
となります。
比例
比例とは
比例とは2つある数の一方が2倍、3倍と増えるにつれ、もう一方も同じように2倍、3倍と増えていくことを比例といいます( ̄▽ ̄)
y=α×xで表すとき、yはxに比例するといいます。
次の表はある人が歩いた時間をx分、進んだ距離をymの関係を表したものです。
| 時間x(分) | 1 | 2 | 3 | 4 | 5 | 6 |
| 進んだ距離y(m) | 50 | 100 | 150 | 200 | 250 | 300 |
表からxが1のときyが50であることがわかります。
これをy=α×xにあてはめると
50=α×1
α=50
表を表す式は
y=50×x となります。
これは1分(x)歩くごとに比例して50m(y)ずつ進むことを表しています。
比例を表すグラフ
次のグラフは上の比例の表をグラフに表したものです。
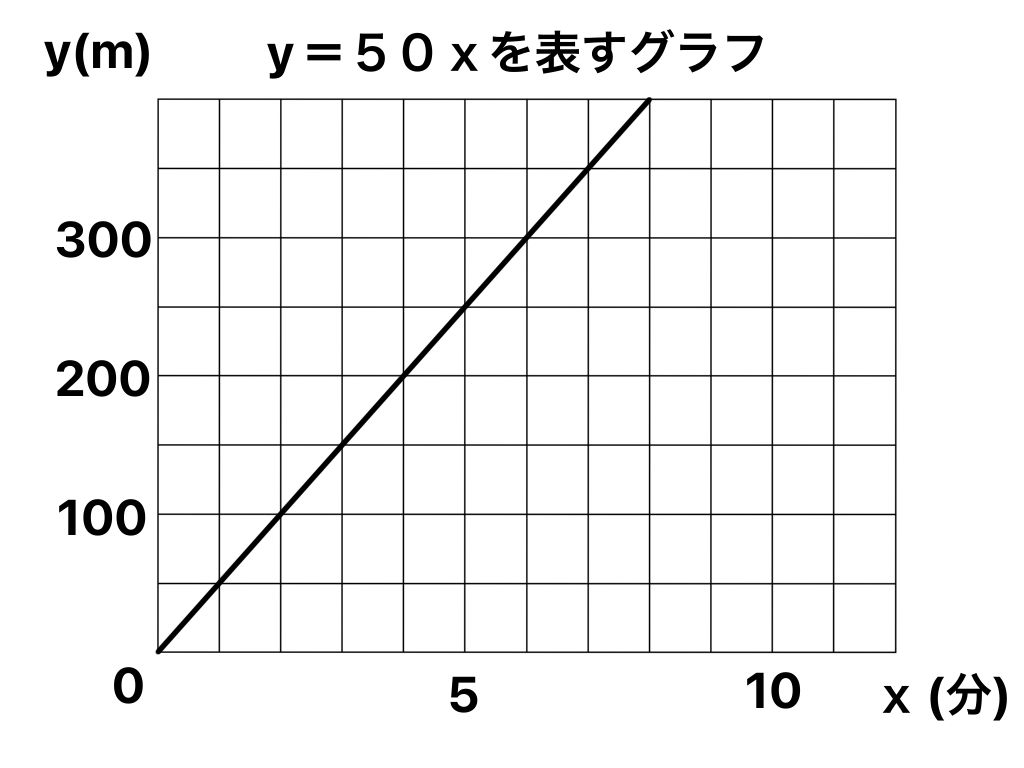
このように比例を表すグラフは上の図のように一直線に伸びていきます( ̄▽ ̄)
x軸を横に、y軸を縦にしグラフを作成します。
反比例
反比例とは
反比例とは2つある数の一方が2倍、3倍と増えるにつれ、もう一方は1/2倍、1/3倍となることを反比例といいます。
反比例を表す式はx×y=αで表すとき、yはxに反比例するといいます。
次の表は反比例を表したものです。
面積30㎥の長方形の縦の長さxm、横の長さymの変化を表したものです。
| 縦の長さx(m) | 1 | 2 | 3 | 5 | 6 | 10 | 15 | 30 |
| 横の長さy(m) | 30 | 15 | 10 | 6 | 5 | 3 | 2 | 1 |
xの値が大きくなるのに反してyの値は小さくなります。
上の表を式で表すと
x×y=30
yを表す式にすると
y=30/x
となります。
反比例を表すグラフ
次のグラフは上の反比例の表をグラフに表したものです。
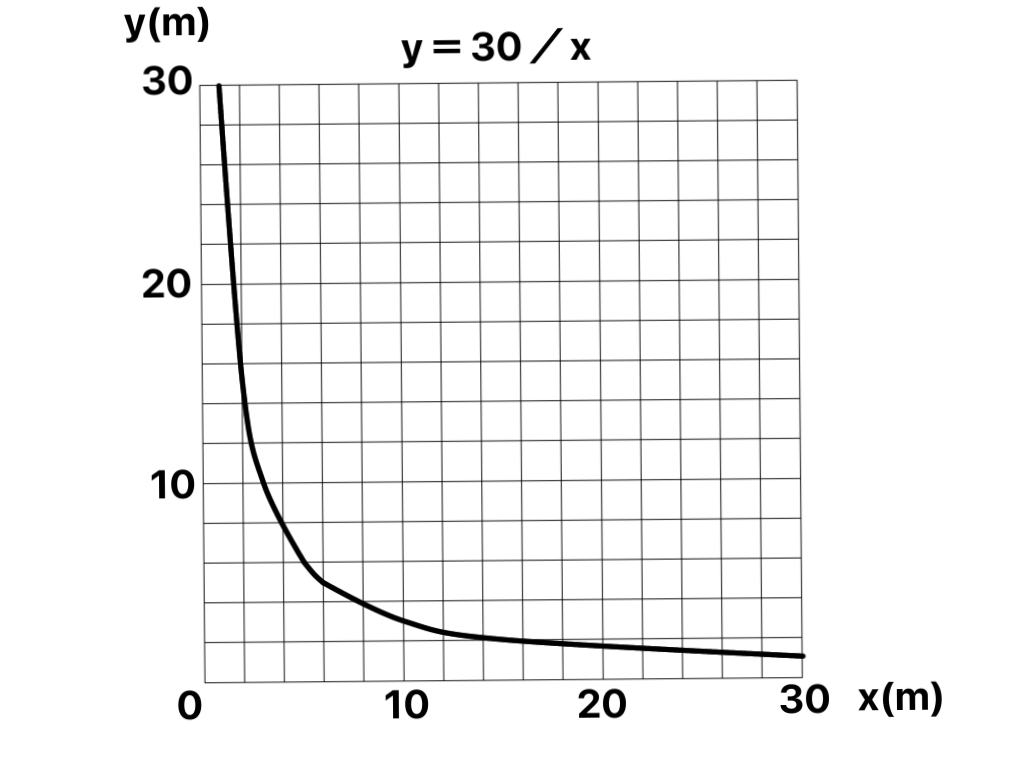
このように反比例を表すグラフは曲線を描きます。
グラフの作り方は、表の値を点でグラフに打ち込み
その点を繋ぐように線を引くと曲線のグラフを描くことができます。
比例、反比例は中学で習ったような…気がするのですが( ̄▽ ̄;)
今は小学校でやるんですね( ̄▽ ̄)
以上!
比・比例・反比例でした( ̄▽ ̄)
大人になった今でも反比例のグラいついつで使うのかわかりません( ̄▽ ̄)
なので復習しないと忘れちゃいますね(*^▽^*)
それでは復習お疲れさまでした!
こいパパでした( ̄▽ ̄)/


