こんにちは!
こいパパです( ̄▽ ̄)
今回は分数の計算について学び直していこうと思います!
分数のたし算
分数のたし算、ひき算には通分を行う必要があります。
まず通分を行い計算していきます。
次の分数の式を通分し計算していきます。
$$\frac{2}{3}+\frac{1}{4}=\frac{8}{12}+\frac{3}{12}$$
通分ができたら分子同士をたし算します。
分母は足さないので注意してください( ̄▽ ̄)
$$=\frac{8+3}{12}=\frac{11}{12}$$
となります。
分母を足さない理由は分数の意味を理解するわかります。
ホールケーキ1/2(半分)が2つあり、足すと1つのホールケーキになります。
しかし分母同士も足してしまうと答えが2/4(半分)となってしまい意味が成り立たなくなります。
なので通分した分母は計算せずに分子同士を計算します。
意味を理解すると計算上でのミスが減りますね( ̄▽ ̄)
分数のひき算
分数のひき算も通分してから行います。
基本的には分数のたし算と一緒ですね( ̄▽ ̄)
$$\frac{2}{3}-\frac{1}{4}=\frac{8}{12}-\frac{3}{12}$$
通分ができたら分子同士をひき算します。
$$=\frac{8-3}{12}=\frac{5}{12}$$
となります。
分数の計算では通分するときの計算ミスに注意しましょう( ̄▽ ̄)
分数のかけ算
分数のかけ算、わり算では通分の必要はありません。
では以下の式を計算していきます。
$$\frac{2}{3}×\frac{1}{4}$$
分数のかけ算では分母同士、分子同士をかけ算します。
$$\frac{2×1}{3×4}=\frac{2}{12}$$
約分して
$$\frac{1}{6}$$
が答えになります。
分数のかけ算では途中式で分母と分子で約分できそうなら約分をしてから計算したほうが、計算が楽になることがあります。
途中式で約分しても答えは一緒になります。
$$\frac{2×1}{3×4}=\frac{(1)×1}{3×(2)}=\frac{1}{6}$$
となります。
しかし分母同士、分子同士では約分できないので注意してください( ̄▽ ̄)
計算後に約分も忘れずに行いましょう( ̄▽ ̄)
【補足】分数・小数のかけ算の意味
分数同士を掛けるといってもパッと意味を理解するのは難しいですよね( ̄▽ ̄)
補足として少しわかりやすく説明してみようかと思います。
ホールケーキで考えてみますね( ̄▽ ̄)
ホールケーキ1/2(半分)を2つ用意するとホールケーキ1つ分になりますよね。
2という数字は分数で表すと2/1となります。
これを式に表すとこうなります。
$$\frac{1}{2}×\frac{2}{1}=\frac{2}{2}$$
つまり1、ホールケーキ1つ分となります。
もう少し説明してみます。
分数(または小数)を掛けるという意味はどういうことでしょう。
1/2倍や0.5倍の意味を理解していきましょう。
またまたホールケーキでイメージしていきますね( ̄▽ ̄)
ちなみに1/2と0.5という数は表記が違うだけで値は同じです。
どちらも半分という意味です。
ではホールケーキが1/2(半分)あります。
これに1/2を掛けるということは1/2(半分)の数を求めたいということです。
1/2(半分のケーキ)の1/2(半分)の数を求めたいという意味です。
ホールケーキ半分の半分は1/4ですよね。
なのでこれを式に表すと
$$\frac{1}{2}×\frac{1}{2}=\frac{1}{4}$$
といことになります。
当時は分数のかけ算の意味を深く理解していませんでした( ̄▽ ̄;)
正しく計算すると答えは出るので( ̄▽ ̄)笑
自分でも調べていてとても勉強になります!
意味としては上記の通りで簡単に言えば、難しく考えなければならないことを式にして計算すれば簡単に求めることができるということですね(*^▽^*)
分数のわり算
分数のわり算なのですが、これは一癖あり割る分数を逆数にし掛け合わせる必要があります。
逆数とは掛け合わせると1になる数です。
分数の場合は分母と分子を逆転させたら逆数になります( ̄▽ ̄)
では次の式を計算していきます。
$$\frac{2}{3}÷\frac{1}{4}$$
この割る分数を逆数にし計算していきます。
$$\frac{2}{3}×\frac{4}{1}=\frac{8}{3}=2\frac{2}{3}$$
となります。
【補足】分数で割るときなぜ逆数にするか
分数で割るときなぜ逆数にするのか考えてみましょう。
これに関してはぼく自身も計算方法としては知っているけど意味を理解はしていませんでした( ̄▽ ̄;)
なのでいろいろ調べて自分なりに勉強してみました。
まずはイメージをとらえていきます。
10/4ℓを2/4ℓずつに分けると何人に配ることができるかを考えていきます。
10/4ℓは1ℓのカップに入れると1ℓ2つと2/4ℓで表せます。
そして2/4ℓずつ分けていくと
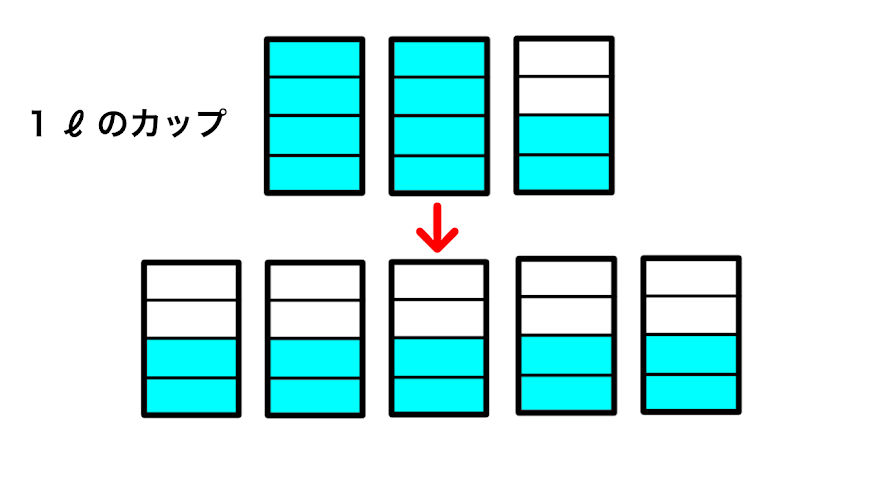
このように5人配ることができます。
式で表すと
$$\frac{10}{4}÷\frac{2}{4}=\frac{10}{4}×\frac{4}{2}=5$$
となります。
では次に逆数にする意味ですが
1÷2=1/2と表すことができます。
なので10/4÷2/4を
$$\frac{\frac{10}{4}}{\frac{2}{4}}$$
と表すことができます。
そして通分の時同様計算しやすくするために分母と分子に4/2を掛けます。
通分についてはこちらで説明しています。
$$\frac{\frac{10}{4}×\frac{4}{2}}{\frac{2}{4}×\frac{4}{2}}=\frac{10}{4}×\frac{4}{2}$$
となります。
このことから分数で割るときは逆数で掛けることで答えが求められることがわかります。
子供に教える時ちゃんと理解してくれるか不安ですね( ̄▽ ̄;)
小数と分数の計算
小数と分数の混じった計算は小数を分数に直して分数同士を計算します。
もしくは分数を小数にし小数同士を計算します。
では2/3+0.9-3/5で考えていきましょう。
小数を分数に直して通分を行ってから計算します。
$$\frac{2}{3}+0.9-\frac{3}{5}=\frac{2}{3}+\frac{9}{10}-\frac{3}{5}$$
$$=\frac{20}{30}+\frac{27}{30}-\frac{18}{30}=\frac{29}{30}$$
小数を分数に直すポイント!
0.1=1/10
0.01=1/100
0.001=1/1000
これがわかっていたら小数を分数に直すのは簡単です!
以上!
分数の計算でした(*^_^*)
意外と多くのことを学ぶことができました!
今までどっちかというと理数系と言っていた自分を恥じたくなります( ̄▽ ̄;)
それでは復習お疲れさまでした!
こいパパでした( ̄▽ ̄)/


