【小学校の算数⑪】線対称・点対称

こんにちは
こいパパです(￣▽￣)

今回は図形の線対称、点対称についてやり直し学習していこうと思います！

線対称

線対称の図形について下の図を例にみていきましょう(￣▽￣)

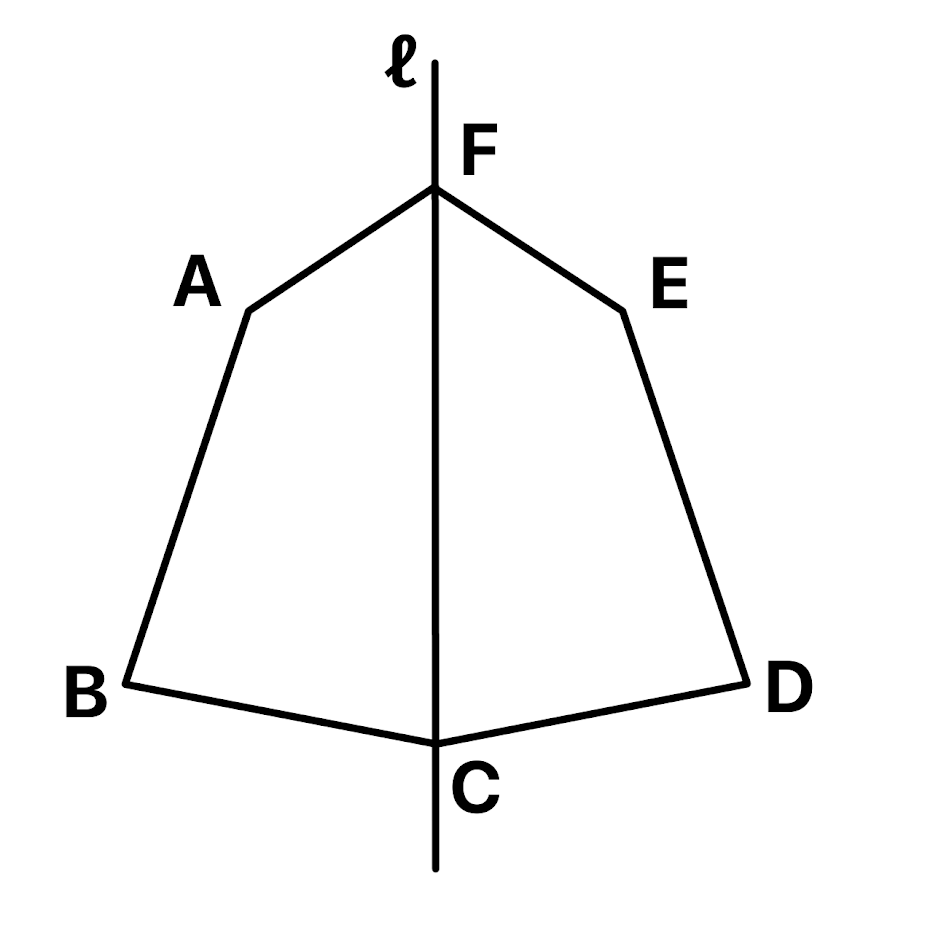
平面の図形に線を引いて、線の左側と右側が左右対称なる図形のことを線対称の図形といいます。
上の図では線ℓを対称の軸としたとき、上の図形は線対称であるといえます(*^_^*)

左右が対称の図形とは、対称の軸を折り目に折ったときにピッタリ重なる図形のことです(*^_^*)

線対称である図形には対称の軸に対しての対応する辺と角があります。
下の図は線対称である図形の対応する辺と角同時を同じ色で表したものです(￣▽￣)

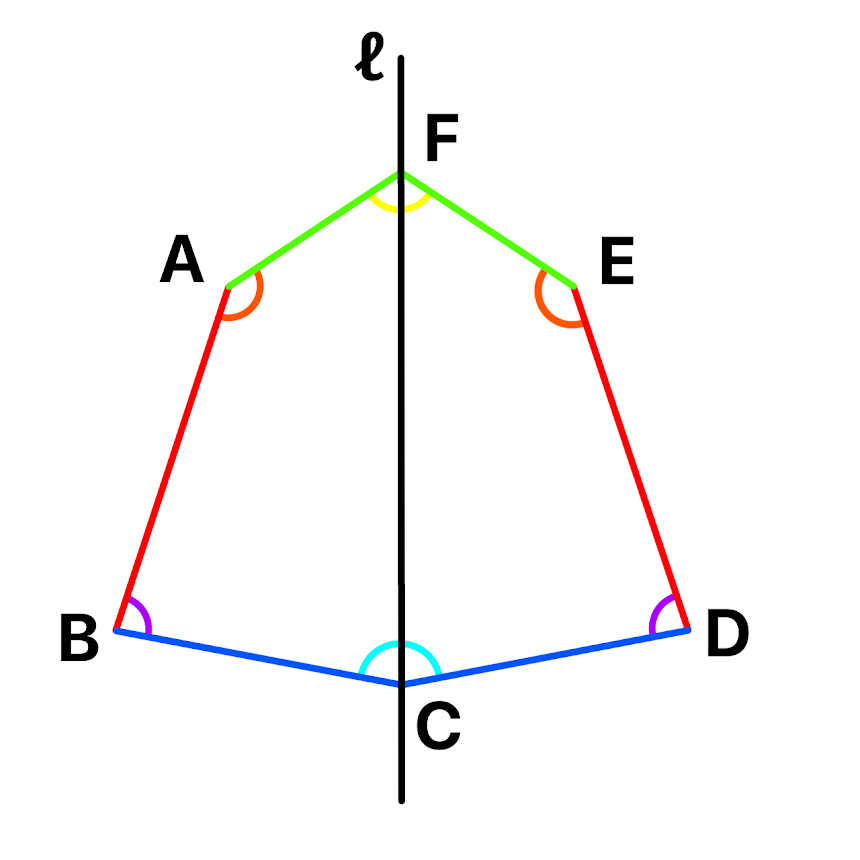
上の図から見てわかるように
辺ABに対応する辺は辺EDとなります。

Aに対応する角はEとなります(￣▽￣)

対応している辺同士の長さは同じです(*^_^*)
対応している角同士の角度も同じです(￣▽￣)

【例題】
『対称の軸をℓとして線対称の図形を描きなさい』

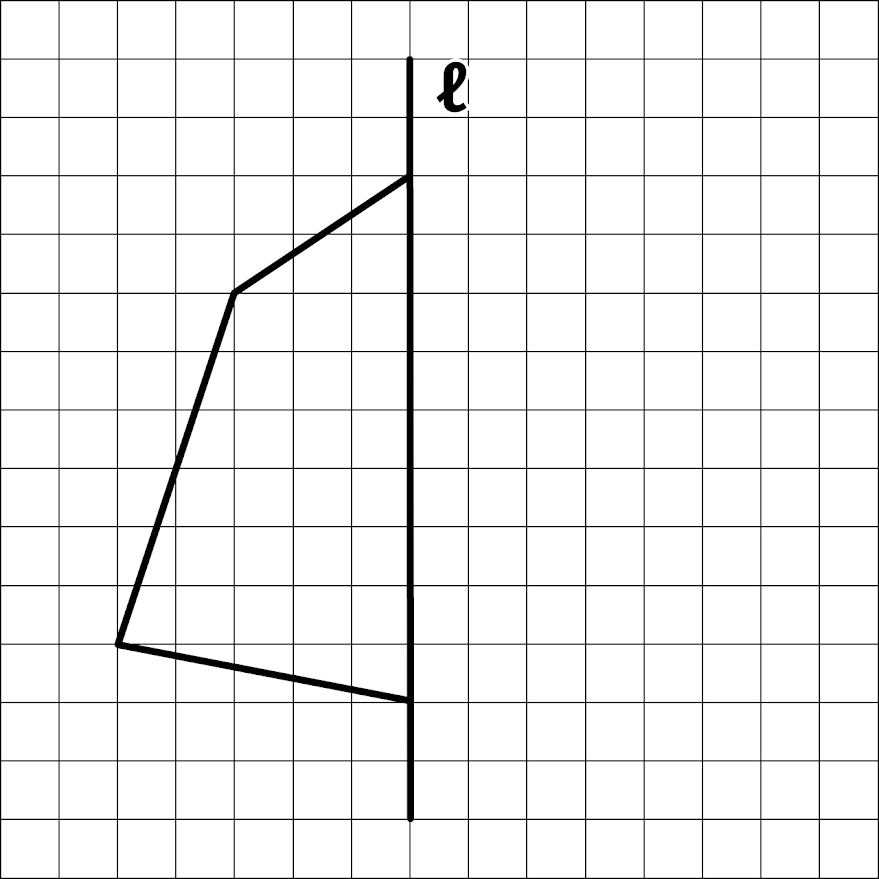
この問題は線ℓを対称の軸とし線対称の図形を描くので、線ℓの右側にも同じ図形を描き入れます。
まず左側の図を参考にし角が方眼の何マス目にくるのかを確認し、右側に対応する角になる点を書き込みます。

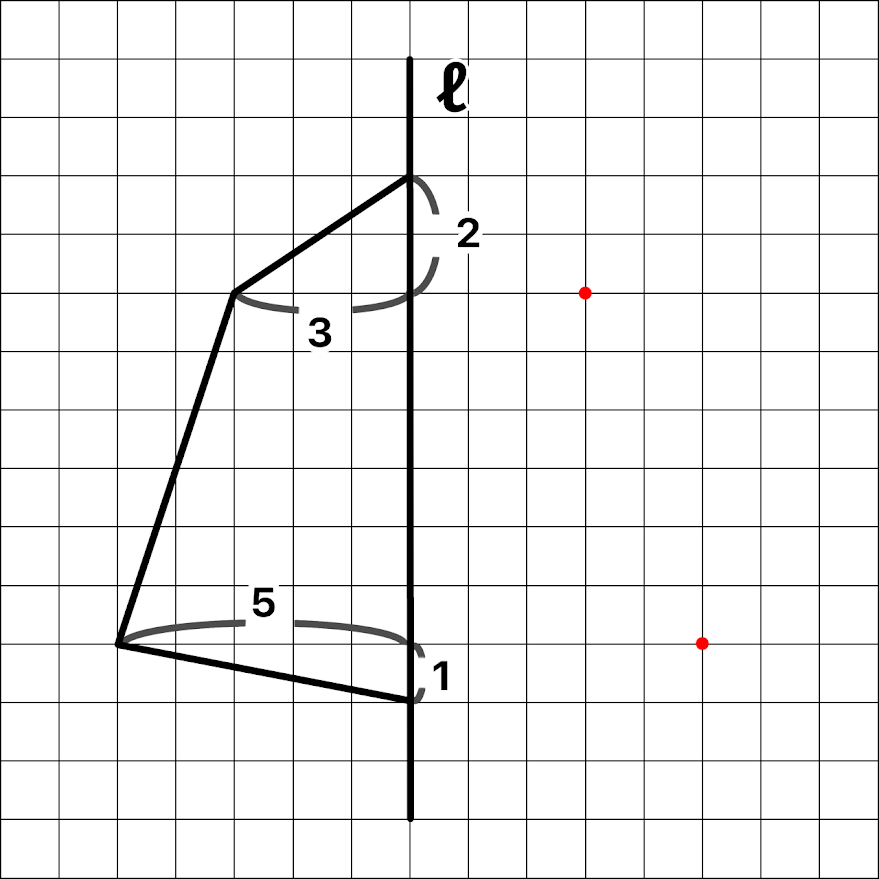
上の図のように対応する角となる点を書き込んだら、その点をもとに線を引いていきます。

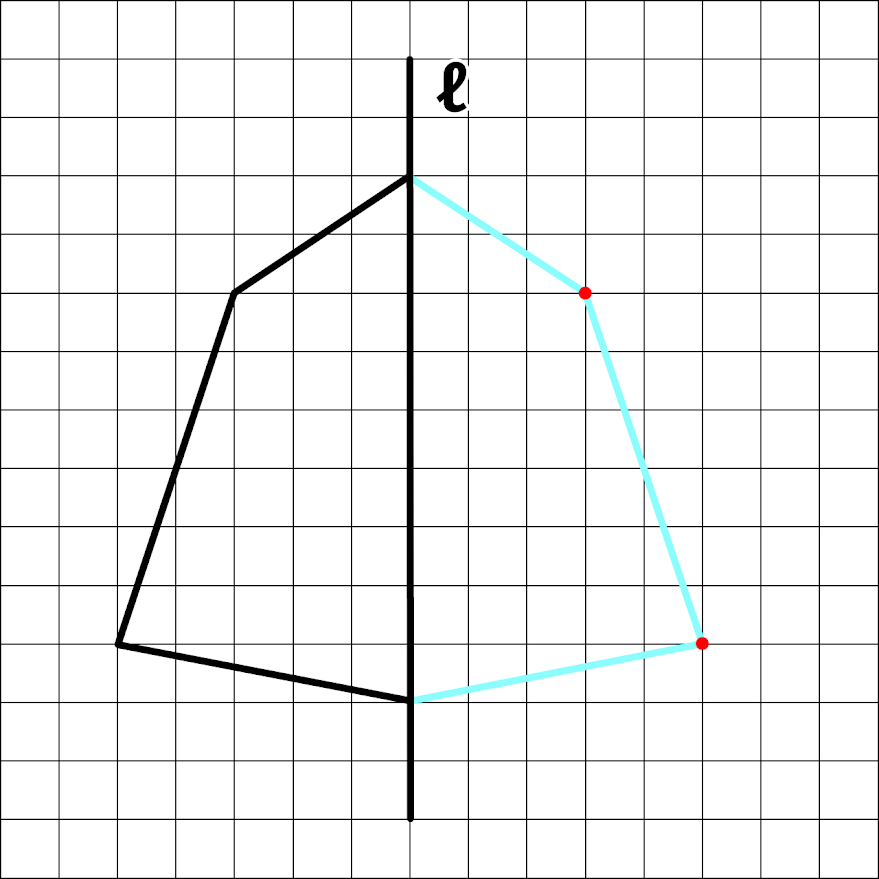
これで対称の軸をℓとした線対称の図形を描くことができます(￣▽￣)

点対称の図形も図を例にみていきましょう(￣▽￣)

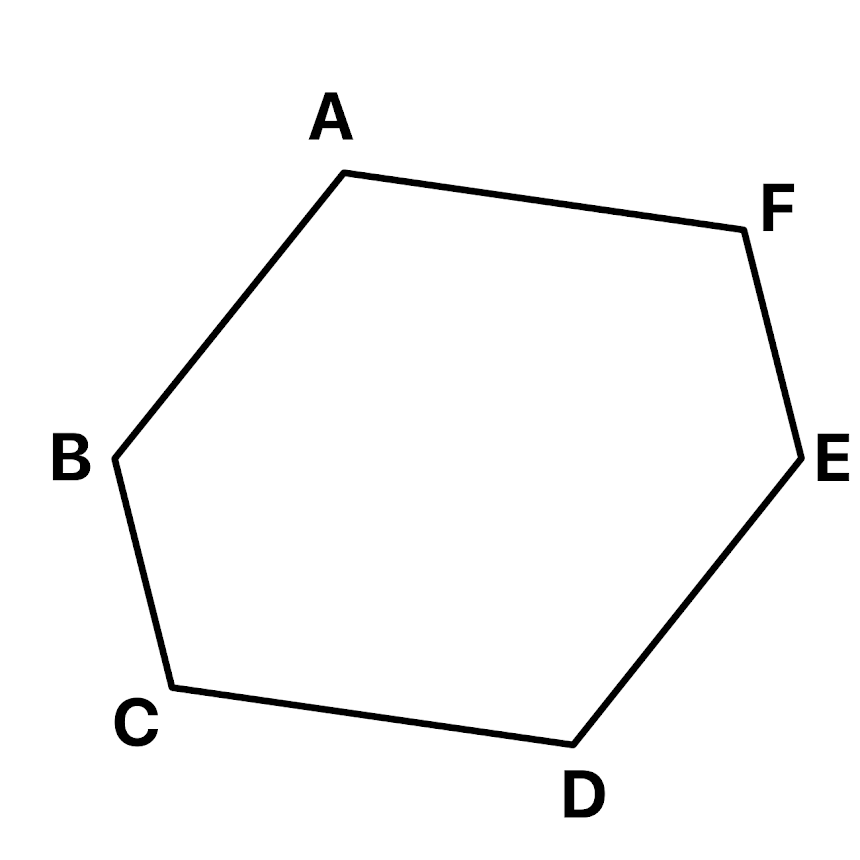
上の図形は点対称の図形です(*^▽^*)
では順を追って点対称の説明をしていきましょう。

まず向かう点同士を線で結んでいきます。

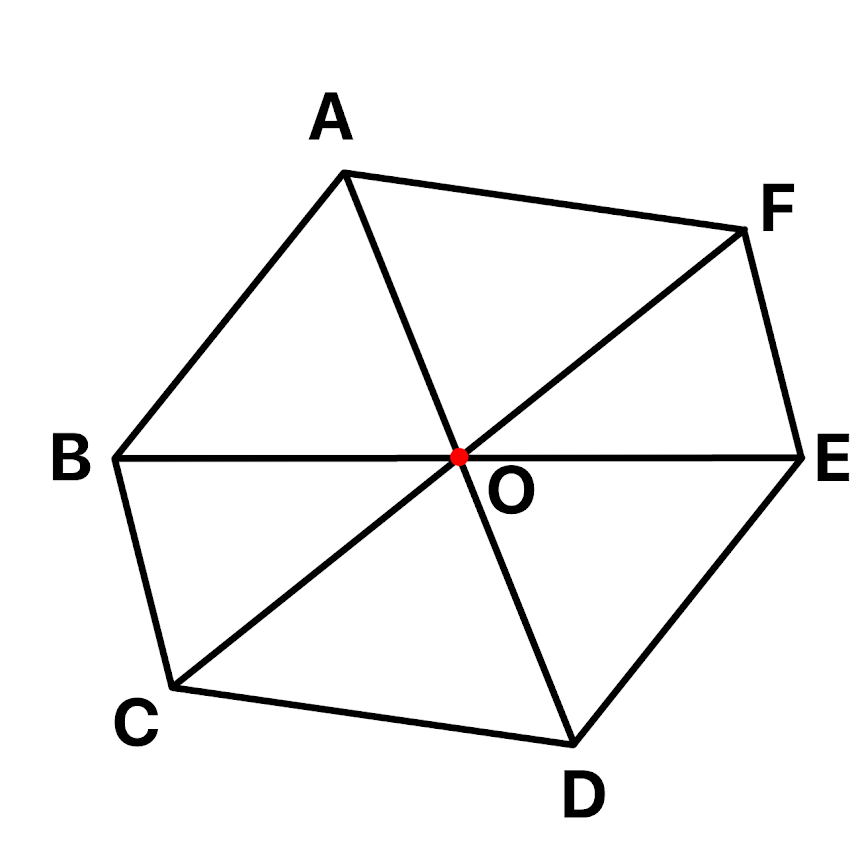
そうするとこのように線が交わる点ができます。
この点Oが対称の中心となります。

この点Oを中心に１８０°回転させてもピッタリ重なります。

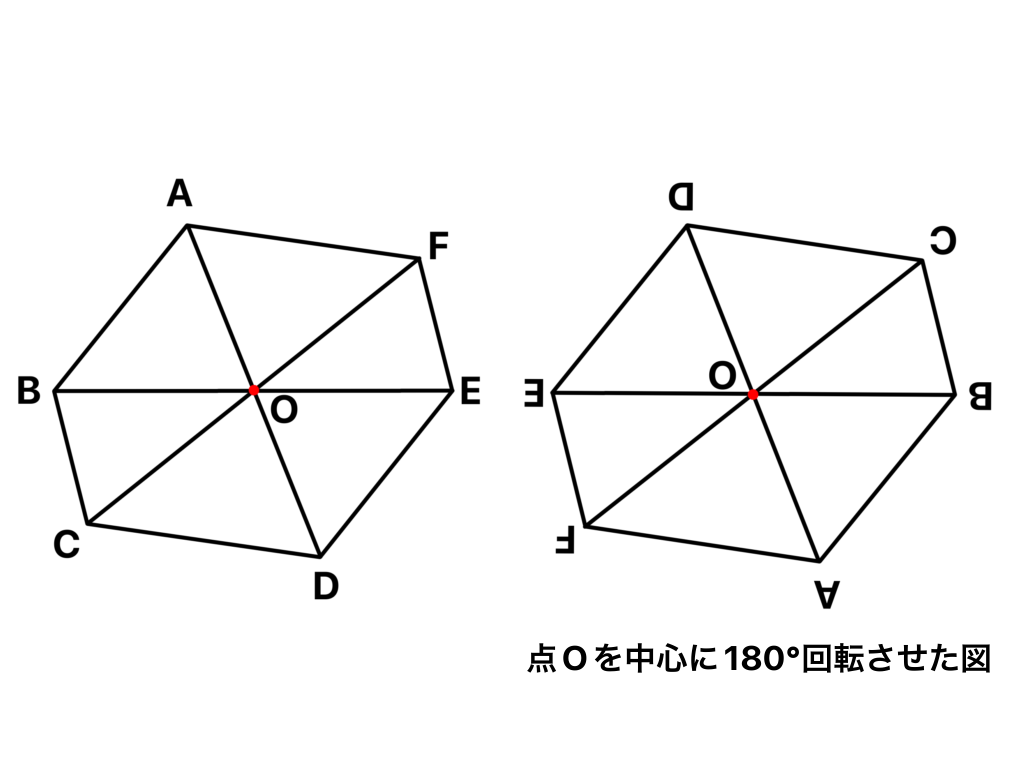
この図のように半回転させても全く同じ形になります。
このような図形を点対称であるといいます(*^_^*)

線対称の図形同様、点対称の図形にも対応する辺と角があります(￣▽￣)
以下の図は点対称の図形の対応する辺と角同士を色分けした図です。

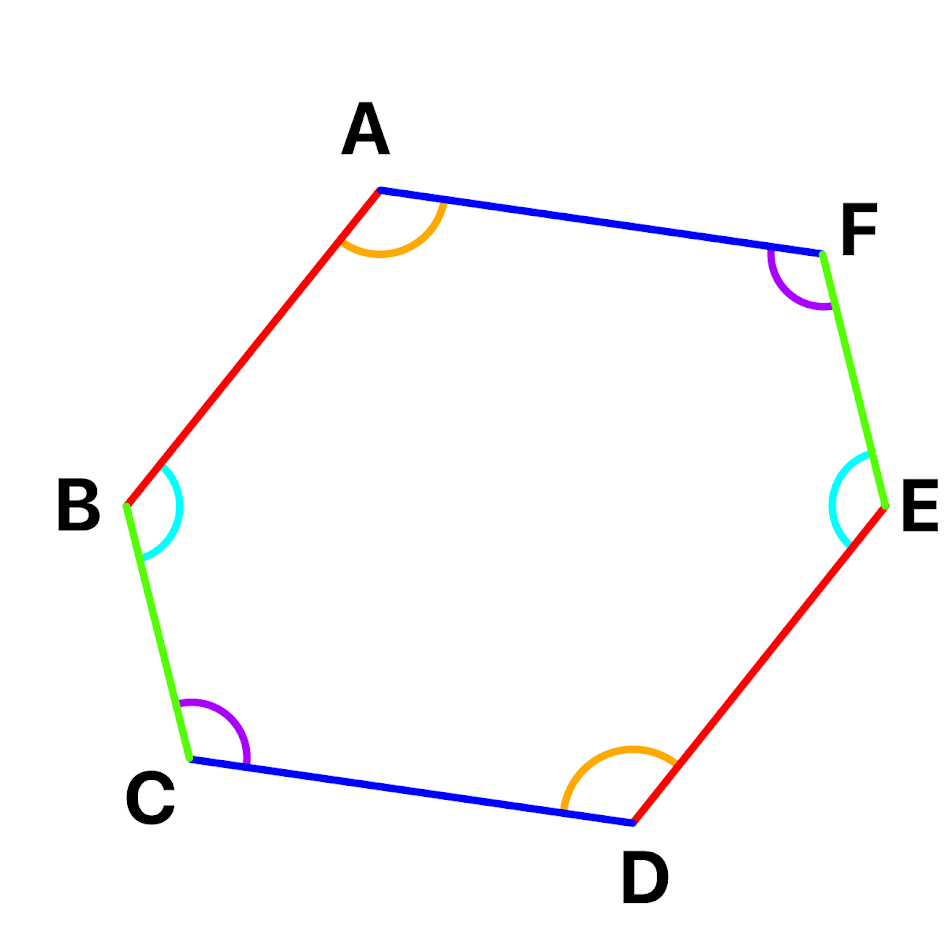
上の図から解るように点対称である図は
向かい合う辺、角同士が対応しています(*^_^*)

以上！
線対称と点対称でした(￣▽￣)

どれも大人になってから見ることが無いものばかりですね！
それゆえに子供に聞かれたら「わからん」と答えるしかないですね(￣▽￣)

この復習記録が誰かのためになっていたらこれ幸いです(*^▽^*)

それでは復習お疲れさまでした！
こいパパでした(￣▽￣)／